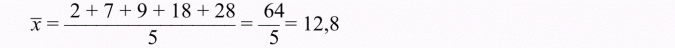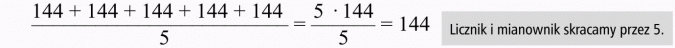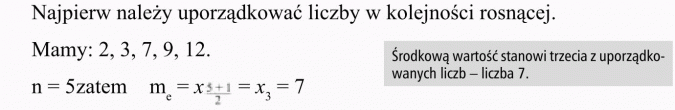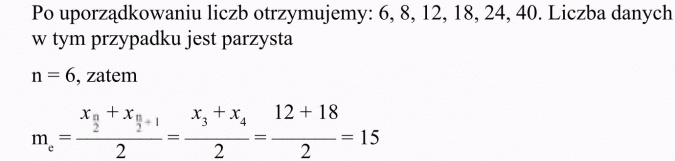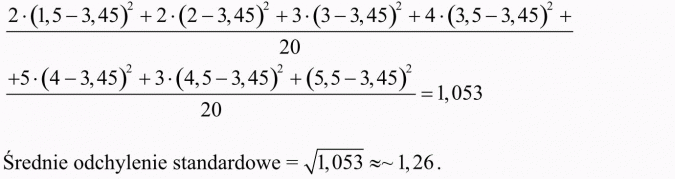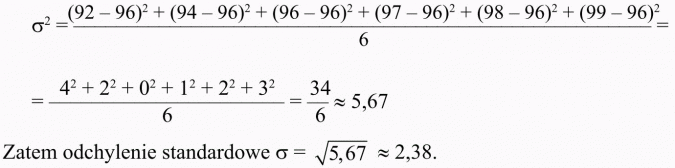Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Zapamiętaj!
Oblicz średnią arytmetyczną z liczb 2, 7, 9, 18 i 28.
Rozwiązanie:
Odpowiedź
Średnia arytmetyczna z danych liczb wynosi 12,8.
Uwaga!
Średnia arytmetyczna z ciągu złożonego z tej samej liczby jest równa tej liczbie.
Średnia z liczb: 144, 144, 144, 144, 144 wynosi 144, bo:
Zapamiętaj!
W pewnej klasie uzyskano następujące oceny ze sprawdzianu: celujący - jedna osoba, bdb - 3 osoby, db - 4 osoby, dst - 8 osób, dop - 7 osób, ndst - 2 osoby. Oblicz średnią ocenę ze sprawdzianu.
Rozwiązanie:
Mamy tutaj do czynienia ze średnią ważoną z ocen: 1, 2, 3,4, 5, 6. Wartościami są tutaj oceny, wagami natomiast są liczebności wystąpienia poszczególnych ocen.
Odpowiedź
Średnia ocen ze sprawdzianu w tej klasie wynosi 3,08.
Pewien uczeń w I semestrze uzyskał z matematyki z prac pisemnych oceny: 3, 3, 3, natomiast z odpowiedzi: 5, 5. Oblicz średnią ocenę tego ucznia.
Rozwiązanie:
Średnia ocena z prac pisemnych równa jest 3, a z odpowiedzi ustnych 5. Średnią ze wszystkich ocen obliczymy ze wzoru:
Odpowiedź
Średnia ocena ucznia równa jest 3,8.
Zapamiętaj!
Dominantą (modą) nazywamy wartość występującą najczęściej.
Podaj dominantę z następujących liczb:
a) 7, -2, 4, 7, 0, 7, 4,
b) 1, 5, 6, 1, 6, 5, 2, 6, 5, 1, 6, 5, 2, 2, 1.
Rozwiązanie:
Ad a)
Najczęściej występuje liczba 7.
Ad b)
| Liczba | 1 | 2 | 5 | 6 |
| Częstość występowania | 4 | 3 | 4 | 4 |
Trzy liczby powtarzają się tak samo często, zatem są trzy dominanty. Są to: 1, 5 i 6.
Odpowiedź
W pierwszym przypadku dominantą jest liczba 7, w drugim natomiast są trzy dominanty: 1, 5 i 6.
Uwaga!
W niektórych przypadkach istnieje kilka dominant. Dominanta z ciągu złożonego z tej samej liczby jest równa tej liczbie.
Dominantą z liczb 37, 37, 37, 37, 37 jest liczba 37.
Zapamiętajk!
Medianą (wartością środkową) ozn. me nazywamy tę wartość, która dzieli zbiór danych wartości na dwie części tak, że liczba danych, których wartości zmiennej są mniejsze od mediany, jest równa liczbie danych, których wartości zmiennej są większe od mediany.
Jeśli zbiór danych {x1, x2, ..., xn} jest uporządkowany niemalejąco, to:
a) Podaj medianę z liczb: 2, 7, 12, 3, 9.
Mediana równa jest 7.
b) Oblicz medianę z liczb: 7, 4, 6, 4, 7, 1, 9.
Medianą jest czwarta w kolejności liczba 6.
c) Oblicz medianę z liczb 12, 6, 24, 18, 40, 8.
Medianą jest liczba 15.
Zapamiętaj!
Rozstęp (ozn. R) jest to różnica między największą i najmniejszą z liczb. Jest to jedna z prostszych miar rozrzutu.
Odchylenie średnie (przeciętne) jest to średnia arytmetyczna odchyleń od wartości średniej.
Każdy z 6 zawodników podczas treningu oddał z pistoletu po 10 strzałów do tarczy. Po zsumowaniu punktów każdego zawodnika otrzymano następujące wyniki: 99, 96, 92, 98, 94, 97. Oblicz rozstęp wyników, średni wynik oraz odchylenie przeciętne.
Rozwiązanie:
Odpowiedź
Rozstęp wyników wynosi 7, średni wynik jest równy 96, a odchylenie przeciętne to 2.
Zapamiętaj!
Odchylenie standardowe (ozn. σ) jest pierwiastkiem kwadratowym z wariancji.
W tabeli zestawione zostały informacje dotyczące średnich ocen uzyskanych przez uczniów klas pierwszych ze sprawdzianu z matematyki. Oblicz średnią ocenę z tego sprawdzianu wszystkich uczniów klas pierwszych. Wynik podaj z dokładnością do 0,01.
Odpowiedź
Średnia ocena wszystkich pierwszoklasistów ze sprawdzianu z matematyki w przybliżeniu równa jest 3,02.
Właściciel sklepu może zamówić puszki z groszkiem konserwowym u dwóch różnych dostawców A i B. Poniższe tabelki przedstawiają wyniki badania masy produktu bez zalewy w 10 losowo wybranych puszkach od obydwu dostawców:
Dostawca A
| Masa produktu bez zalewy (g) | 120 | 130 | 135 | 140 |
| Liczba puszek | 1 | 4 | 2 | 3 |
Dostawca B
| Masa produktu bez zalewy (g) | 125 | 135 | 140 | 145 |
| Liczba puszek | 3 | 2 | 4 | 1 |
Oblicz rozstęp i wariancję mas produktu bez zalewy od dostawcy A i B. Oceń, u którego z dostawców powinien zamawiać towar właściciel sklepu.
Rozwiązanie:
Odpowiedź
Rozstęp mas produktu bez zalewy od obu dostawców jest taki sam i wynosi 20. Wariancję mas produktu bez zalewy od dostawcy A wynosi 36, a od dostawcy B równa jest 50. Wynika z tego, że właściciel sklepu powinien wybrać dostawcę A.
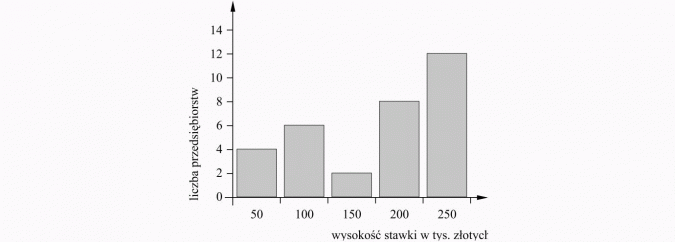
Diagram przedstawia liczbę przedsiębiorstw w pewnej gminie, płacących podatek roczny w określonej wysokości. Oblicz:
a) średnią stawkę podatku rocznego przypadaj ącego na przedsiębiorstwa z tego zestawienia,
b) podatek dominujący,
c) wysokość podatku, którego nie przekracza połowa przedsiębiorstw,
d) rozstęp stawki podatkowej.
Rozwiązanie:
Sporządź diagram kołowy przedstawiający dane dotyczące podatków płaconych przez przedsiębiorstwa, o których mowa jest w zadaniu 7.
Rozwiązanie:
Przed sporządzeniem diagramu, należy obliczyć, jaki procent wszystkich przedsiębiorstw stanowią grupy płacące poszczególne podatki.
Przedsiębiorstwa płacące podatek w wysokości:
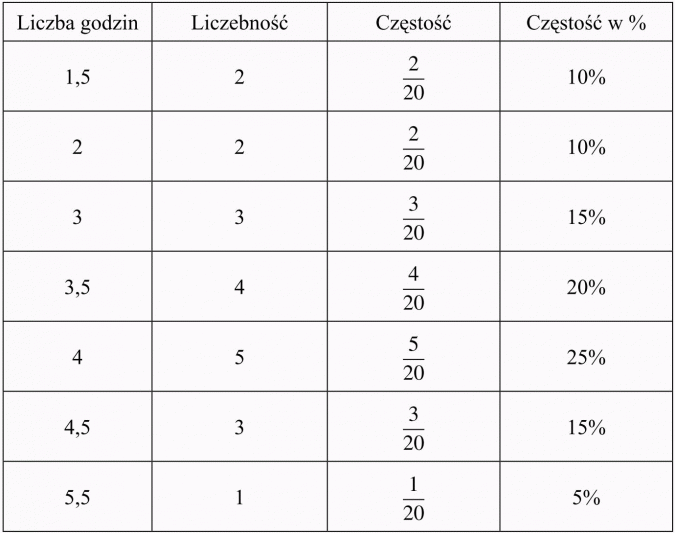
W pewnej klasie liczącej 20 uczniów zebrano dane dotyczące liczby godzin spędzanych dziennie, przez pojedynczego ucznia, przed komputerem. Uzyskano następujące dane (w godzinach):
| 3 | 3,5 | 4,5 | 4,5 | 5,5 | 4 | 3 | 4 | 4,5 | 1,5 | 3,5 | 4 | 2 | 2 | 1,5 | 3,5 | 4 | 3 | 3,5 | 5 |
a) Uporządkuj dane i przedstaw je w postaci histogramu liczebności.
b) Wyznacz średnią arytmetyczną i medianę.
c) Zbuduj szereg rozdzielczy i oblicz średnią ważoną.
d) Dane przedstaw w postaci diagramu kołowego.
e) Wyznacz wariancję i średnie odchylenie standardowe.
Rozwiązanie:
Ad a)
Dane uporządkowane:
| 1,5 | 1,5 | 2 | 2 | 3 | 3 | 3 | 3,5 | 3,5 | 3,5 | 3,5 | 4 | 4 | 4 | 4 | 4 | 4,5 | 4,5 | 4,5 | 5,5 |
Histogram liczebności: (rysunek)
Ad b)
Średnia arytmetyczna:
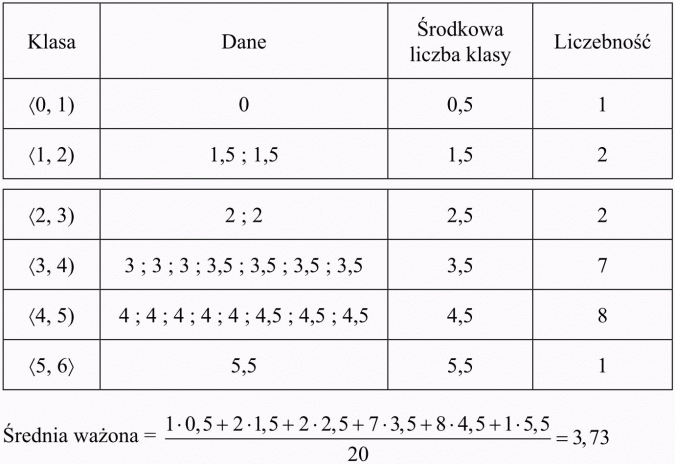
Ad c)
Szereg rozdzielczy:
Ad d)
Diagram kołowy:
Ad e)
Wariancja:
Wróćmy do zadania 5 i obliczmy wariancję wyników uzyskanych przez zawodników podczas treningu:
Uwaga!
Wariancję możemy obliczyć również ze wzoru:
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.