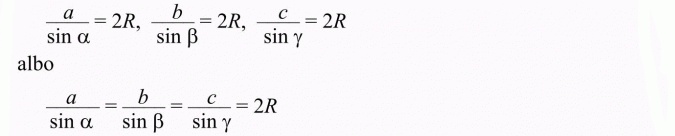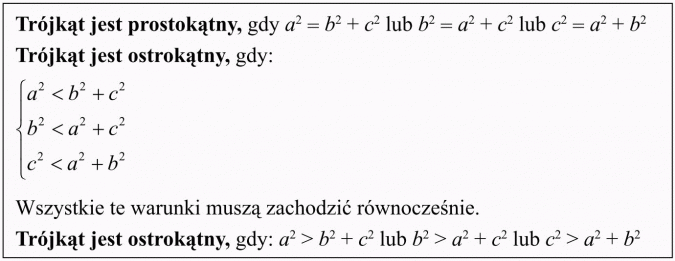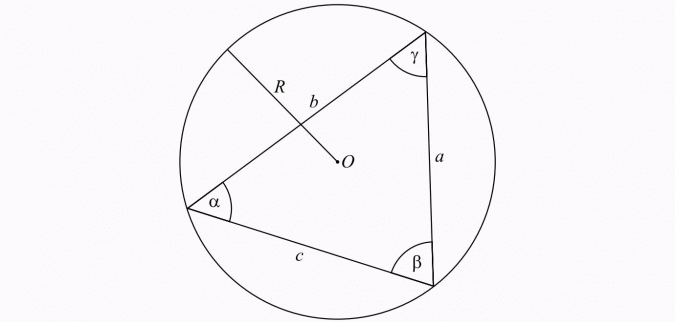
Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów

Twierdzenie sinusów brzmi: w dowolnym trójkącie stosunek długości boku do sinusa kąta leżącego naprzeciw tego boku jest równy średnicy koła opisanego na tym trójkącie.

Inaczej (spójrz na rysunek)

Twierdzenie to służy do tzw. rozwiązywania trójkątów, tzn. znajdowania boków i kątów danych trójkątów.

Zadanie 1

Mając dane długości a, b boków trójkąta ostrokątnego ABC oraz długość R promienia okręgu na nim opisanego, oblicz sinusy kątów oraz długość trzeciego boku trójkąta. Wykonaj obliczenia, gdy a = 6, b = 10, R = 8.

Rozwiązanie:

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. Sporządzamy rysunek, wprowadzamy oznaczenia i dane z zadania. Najpierw spróbujemy znaleźć sin alfa. Korzystamy z tw. sinusów, biorąc pod uwagę: bok a, kąt alfa i promień R. Podstawiamy do wzoru dane z zadania i z równości wyliczamy sin alfa. Korzystamy z tw. sinusów, biorąc pod uwagę bok b, kąt beta i promień R. Podstawiamy do wzoru dane z zadania i z równości wyliczamy sin beta. Teraz znajdziemy miarę kąta gamma. Wiemy z poprzednich rachunków, że... Wartości kątów alfa i beta znajdujemy w tablicach matematycznych lub posługując się kalkulatorem. Wiadomo, że w trójkącie suma kątów równa się 180 st., stąd... Do tej równości podstawiamy znalezione kąty alfa i beta i wyliczmy gamma. Mając dany kąt gamma, znajdujemy jego sinus. Posługujemy się tablicami lub kalkulatorem. Pozostał do wyliczenia bok c. Korzystamy z twierdzenia sinusów, biorąc pod uwagę: bok c, kąt gamma i promień R. Do wzoru podstawiamy dane z zadania i wyliczamy c.

Zadanie 2

W trójkącie ABC bok AB = c = 12, bok BC = a = 10, bok CA = b = 6. Dwusieczna kąta ACB przecina bok AB w punkcie D. Oblicz długości odcinków AD i BD.

Rozwiązanie:

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. Sporządzamy rysunek. Kąty zaznaczone na rysunku jako gamma są równe, bo CD jest dwusieczną (dwusieczna dzieli kąt na dwa kąty przystające). Ponadto suma kątów alfa i beta równa się 180 st. Jest tak dlatego, że alfa i beta to kąty przyległe, a suma kątów przyległych to kąt półpełny (czyli ma 180 st.). Otrzymaliśmy równanie z dwiema niewiadomymi x i y. Chcąc znaleźć te wielkości trzeba napisać drugie równanie, też z niewiadomymi x i y, a następnie ułożyć i rozwiązać układ równań. Korzystamy z tw. sinusów. Te dwa ułamki są równe, bo oba są równe średnicy okręgu opisanego na trójkącie BCD. Następnie (dla potrzeb rozwiązania) wyliczamy... W miejsce a wpisujemy 10, zgodnie z danymi. Korzystamy z tw. sinusów. Następnie (dla potrzeb rozwiązania) wyliczamy... Podstawiamy dane z zadania. Dowodzimy, że sinusy kątów przyległych są równe. Korzystamy ze wzorów redukcyjnych; k= 2, czyli funkcja sinus nie przechodzi w kofunkcję. Kąt alfa ma końcowe ramię w II ćwiartce, a w tej ćwiartce sinus jest dodatni, stąd sin alfa = sin beta. Wobec powyższej uwagi obydwa ułamki są równe. Z pierwszego równania wyliczamy y i podstawiamy do drugiego. W drugim równaniu wykonujemy mnożenie na krzyż i wyliczamy x. Odpowiedź: Szukane odcinki mają długości...

Zadanie 3

Dany jest trójkąt o bokach a, b, c. Promień okręgu opisanego na tym trójkącie równy jest R. Oblicz pole tego trójkąta.

Rozwiązanie:

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. Sporządzamy rysunek, na którym w sposób najbardziej czytelny zaznaczamy dane. Oznaczamy dodatkowo: kąt przy wierzchołku C= gamma, wysokość trójkąta ABC= h. Oznaczamy przez S pole trójkąta. Wielkość tę musimy znaleźć. Korzystamy z podstawowego wzoru na pole trójkąta. Rozważmy trójkąt prostokątny CAD. W tym trójkącie... Korzystamy zdefinicji sinusa kąta ostrego gamma w trójkącie prostokątnym CAD (iloraz przyprostokątnej leżącej naprzeciw kąta ostrego do przeciwprostokątnej). Z równości tej wyliczamy h. Do wzoru na pole trójkąta wstawiamy h = b sin gamma. Zauważamy, że w powyższym wzorze nie znamy jedynie sin gamma. Korzystamy z twierdzenia sinusów. Wybieramy tę równość, w której występuje sin gamma. Wstawiamy sin gamma do wzoru na pole trójkąta. Odpowiedź: Pole trójkąta równa się... W ten sposób wyprowadziliśmy wzór na pole dowolnego trójkąta o bokach długości a, b, c wpisanego w dowolny okrąg o promieniu R. Warto w tym miejscu wspomnieć jeszcze o jednym wzorze na pole trójkąta, tym razem opisanego na okręgu. Pole dowolnego trójkąta o bokach długości a, b, c, w który wpisujemy okrąg o promieniu r, wyraża się następującym wzorem... Pole dowolnego trójkąta opisanego na okręgu, to iloczyn połowy obwodu trójkąta i promienia okręgu wpisanego w ten trójkąt. Czasami możesz się spotkać z inną postacią tego wzoru, mianowicie... To połowa obwodu trójkąta.

Zadanie 4

W trójkącie ABC mamy dane: długości boków AB i AC, długość r promienia okręgu wpisanego oraz miarę kąta α. Oblicz: długość boku BC, miary kątów β i γ, pole trójkąta ABC i długość promienia okręgu opisanego na trójkącie.

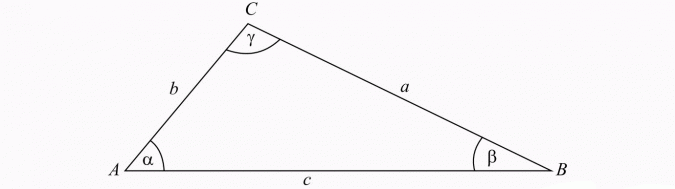
Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. Wykonaj obliczenia dla... Sporządzamy rysunek, wprowadzając wygodniejsze oznaczenia... Promień okręgu wpisanego w ten trójkąt jest prostopadły do boku! Zanim przystąpimy do rozwiązania, sporządzamy plan pracy. Obliczmy pole S trójkąta ABC. Obliczmy pole trójkąta w zależności od długości jego trzech boków i promienia okręgu wpisanego. To pozwoli nam obliczyć trzeci bok BC trójkąta. Korzystając ze wzoru... obliczymy promień R okręgu opisanego. Z twierdzenia sinusów obliczymy miary kątów... Stosujemy wzór na pole trójkąta, który wykorzystuje iloczyn dwóch danych boków i sinus kąta alfa zawartego między nimi. Do wzoru wstawiamy dane. Ze wzorów redukcyjnych... Popatrz na rysunek: w każdym z trzech małych trójkątów r (promień okręgu wpisanego) jest wysokością, bo jest prostopadły do boku w punkcie styczności okręgu z bokiem. Stąd właśnie wzór... Pole każdego z małych trójkątów można wyliczyć oddzielnie, stosując wzór na pole trójkąta. Do wzoru wstawiamy dane. Teraz porównujemy obydwa wzory na pole tego samego trójkąta i wyliczamy a. Dany trójkąt ma pole zawsze takie samo niezależnie od tego, jakim wzorem się posługujemy. Dlatego można ... porównać. Wyliczamy a. Stosujemy wzór na pole trójkąta, znaleziony w poprzednim zadaniu. Wyliczamy z tego wzoru R. Podstawiamy do wzoru dane. Korzystamy z tw. sinusów. Do wzoru podstawiamy dane.

Twierdzenie cosinusów

W dowolnym trójkącie między bokami i kątami zachodzą związki:

a² = b² + c² - 2bc cos α

b² = a² + c² - 2ac cos β

c² = a² + b² - 2ab cos γ

(kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn tych boków i cosinusa kąta zawartego między nimi).

Bardzo ważny wniosek z twierdzenia cosinusów

Twierdzenie cosinusów pozwala rozstrzygnąć, czy dany trójkąt jest ostrokątny, prostokątny czy rozwartokątny.

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. Trójkąt jest prostokątny, gdy... Trójkąt jest ostrokątny, gdy... Wszystkie te warunki muszą zachodzić równocześnie.

Zadanie 5

Sprawdź, czy trójkąt o wierzchołkach A(1, 5), B(3, 2), C(-6, -4) jest prostokątny.

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. W rozwiązaniu zadania skorzystamy z następującego rozumowania: jeśli po obliczeniu długości boków danego trójkąta okaże się, że kwadrat któregoś boku jest równy sumie kwadratów boków pozostałych, to zgodnie z twierdzeniem odwrotnym do tw. Pitagorasa dany trójkąt będzie prostokątny. Rysunek pełni rolę pomocniczą. Najpierw policzymy długości boków trójkąta. Przy obliczaniu długości korzystamy ze wzoru... Teraz należy zauważyć, że... Po podniesieniu do kwadratu...

Odpowiedź

Trójkąt jest prostokątny (ma kąt prosty przy wierzchołku B, czyli bok AC jest przeciwprostokątną w tym trójkącie).

Zadanie 6

Sprawdź, czy trójkąt o wierzchołkach P(-1, 2), Q(1, -2), R(2, -4) jest prostokątny.

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. Najpierw liczymy długości boków trójkąta. Sposób postępowania jest analogiczny do poprzedniego. W rozumowaniu posługujemy się twierdzeniem odwrotnym do tw. Pitagorasa. Posługujemy się wzorem... Teraz sprawdzamy, czy kwadrat któregoś boku jest równy sumie kwadratów boków pozostałych. Podstawiamy do wzorów dane, pamiętając, że...

Odpowiedź

Trójkąt PQR nie jest prostokątny

Zadanie 7

Boki AB i AC trójkąta ABC mają odpowiednie długości 4 i 6 i tworzą kąt BAC o mierze 120°. Oblicz długość boku BC tego trójkąta.

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. Sporządzamy rysunek, zaznaczamy dane i przez x oznaczamy dtugość szukanego boku BC Jest to typowa sytuacja, w której trzeba zastosować tw. cosinusów. Do wzoru cosinusów wstawiamy dane. Trzeba wyliczyć cos 120 st. posługując się wzorami redukcyjnymi. 120 st. przedstawiamy w postaci 2-90 st. - 60st., k= 2, a = 60 st. Ponieważ k= 2 funkcja cosinus pozostaje bez zmian. 120 st. ma końcowe ramię w II ćwiartce, w której cosinus jest ujemny, stąd mamy -cos 60 st., czyli -1/2.

Zadanie 8

Oblicz kąty trójkąta ABC, w którym AB = 7, BC = 11, CA = 14. Rozstrzygnij, czy trójkąt jest ostrokątny, prostokątny czy rozwartokątny.

Rozwiązanie:

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. W rozwiązaniu wykorzystujemy trzykrotnie twierdzenie cosinusów. Można to zrobić, dlatego że dane są długości wszystkich boków trójkąta. Sformułowanie Oblicz kąty jest równoważne znajdź cosinusy tych kątów. Stosujemy twierdzenie cosinusów, wyróżniając najpierw AB. Teraz wyróżniamy AC. Teraz wyróżniamy BC. Ponieważ cos B mniejsze od 0, kąt B jest rozwarty (cosinus jest ujemny w II ćwiartce, B może być kątem II ćwiartki, bo jest kątem trójkąta).

Trójkąt jest rozwartokątny i ma kąt rozwarty przy wierzchołku B.

Pamietaj!

Warto znać twierdzenie dotyczące zależności pomiędzy miarami kątów wewnętrznych w trójkącie i długościami jego boków.

Twierdzenie

W dowolnym trójkącie naprzeciw największego kąta leży najdłuższy bok i na odwrót, czyli naprzeciw najdłuższego boku znajduje się kąt o największej mierze.

Zatem na podstawie tego twierdzenia rozwiązanie zadania 8 można bardzo uprościć. Wystarczy bowiem obliczyć wartość cosinusa kąta B leżącego naprzeciw najdłuższego boku (u nas bok CA = 14). Jedynie ten kąt może być rozwarty, co pociąga za sobą fakt, że trójkąt może wówczas być rozwartokątny.

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. ..., czyli miara kąta B jest największa, zatem kąt B jest rozwarty.

Pomijamy pozostałe przypadki, ponieważ stwierdzamy definitywnie, iż trójkąt jest rozwartokątny.

Zadanie 9

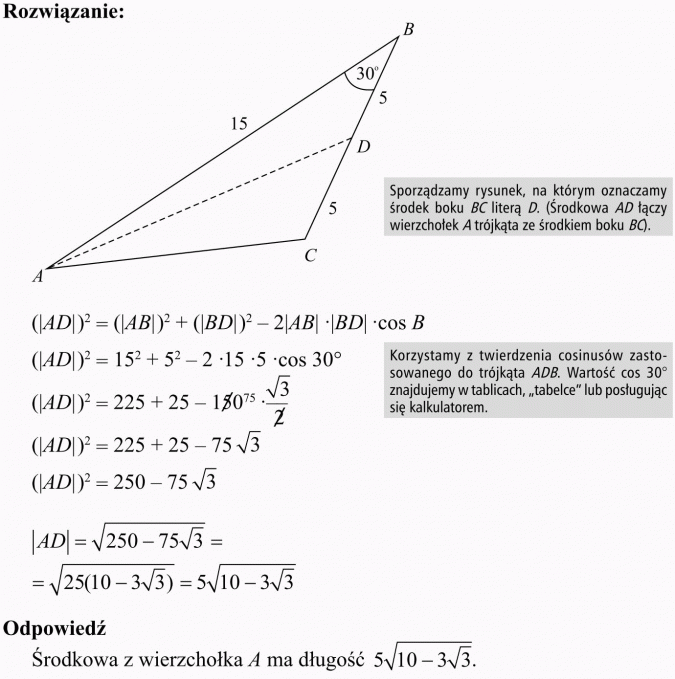
W trójkącie ABC, AB = 15, BC = 10, B = 30°. Znajdź długość środkowej poprowadzonej z wierzchołka A.

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów. Sporządzamy rysunek, na którym oznaczamy środek boku BC literą D. (Środkowa AD łączy wierzchołek A trójkąta ze środkiem boku BC). Korzystamy z twierdzenia cosinusów zastosowanego do trójkąta ADB. Wartość cos 30 st. znajdujemy w tablicach, tabelce lub posługując się kalkulatorem. Odpowiedź: Środkowa z wierzchołka A ma długość...

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Rozwiązywanie trójkątów z zastosowaniem twierdzenia sinusów i cosinusów