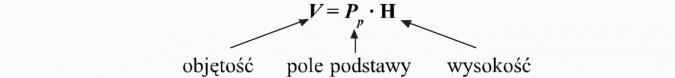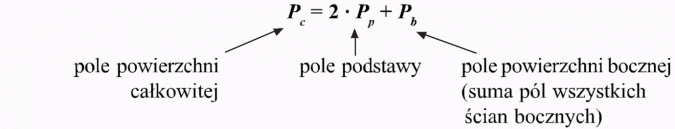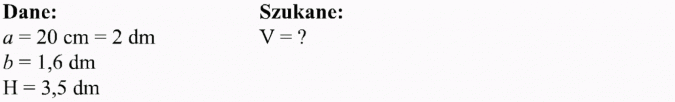Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Graniastosłup czworokątny (podstawa graniastosłupa jest czworokątem).
Graniastosłup trójkątny (podstawa graniastosłupa jest trójkątem).
Objętość graniastosłupa:
Pole powierzchni całkowitej:
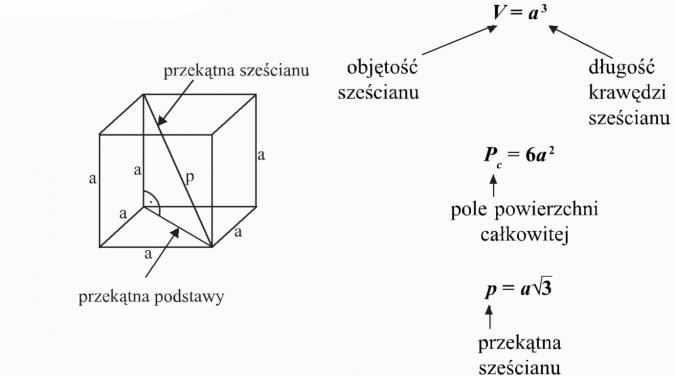
Sześcian
Odp.: Objętość prostopadłościanu wynosi 100 cm3, a pole powierzchni całkowitej 160 cm2.
Oblicz długość krawędzi sześcianu o objętości 64 cm3. Jaką długość ma jego przekątna?
Rozwiązanie:
Odp.: Objętość graniastosłupa wynosi 750 cm3.
Długość przekątnej sześcianu o krawędzi długości 10 cm można obliczyć również inaczej (w razie gdybyśmy zapomnieli wzór):
Odp.: Objętość graniastosłupa wynosi 36 cm3, a pole powierzchni 66 cm2.
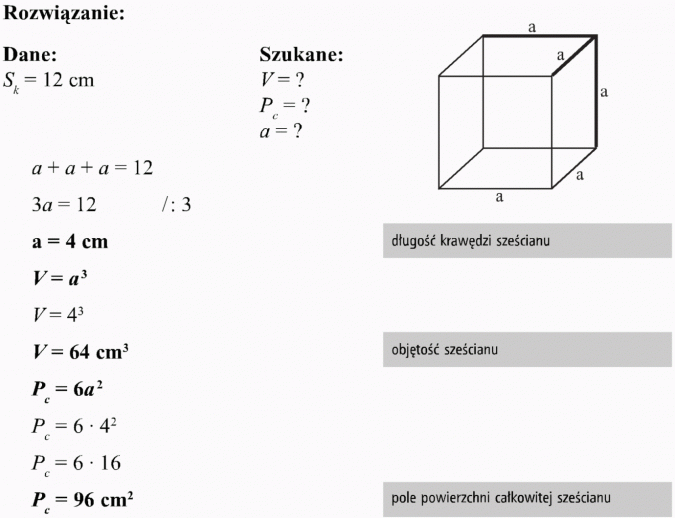
Suma długości trzech krawędzi sześcianu wychodzących z jednego wierzchołka jest równa 12 cm. Oblicz objętość i pole powierzchni całkowitej tego sześcianu.
Odp.: Objętość sześcianu wynosi 64 cm3, a jego pole powierzchni 96 cm2.
Basen ma kształt prostopadłościanu, którego długość jest równa 20 m, a szerokość 15 m. Do basenu wlano 225 m3 wody. Oblicz wysokość wody w basenie.
Odp.: Wysokość wody w basenie wynosi 75 cm.
Czy 15 litrów wody zmieści się w akwarium o wymiarach 20 cm x 1,6 dm x 3,5 dm?
Rozwiązanie:
Wymiary akwarium należy sprowadzić do jednakowych jednostek. Pytamy o litry, wygodnie jest więc wymiary akwarium podać w decymetrach, bo
Odp.: Nie zmieści się.
Odp.: Potrzeba 7 puszek farby.
Odp.: Wlano 40 l wody.
Do zbiornika w kształcie prostopadłościanu o wymiarach 12 m x 8,25 m x 3 m nalano 74 250 l wody.
Oblicz:
a) ile litrów może pomieścić ten zbiornik
b) w ilu procentach został wykorzystany ten zbiornik.
Rozwiązanie:
Odp.: Zbiornik został wykorzystany w 25%.
W prawidłowym graniastosłupie trójkątnym krawędź podstawy ma długość 4 cm, a krawędź boczna 3 cm. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Rozwiązanie:
1 dm3 drewna waży 0,8 kg. Oblicz, ile waży deska dębowa o długości 2 m, szerokości 3 cm i grubości 6 cm.
Rozwiązanie:
Podstawą graniastosłupa prostego jest trójkąt równoboczny o boku 5 cm. Przekątna ściany bocznej jest nachylona do płaszczyzny podstawy pod kątem 45°. Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
Rozwiązanie:
Po wykonaniu rysunku bryły i naniesieniu danych dobrze jest wykonać rysunki pomocnicze podstawy oraz powstałego trójkąta prostokątnego.
podstawa graniastosłupa (kwadrat):
Wysokość H graniastosłupa obliczamy z powstałego trójkąta prostokątnego:
Rozwiązanie:
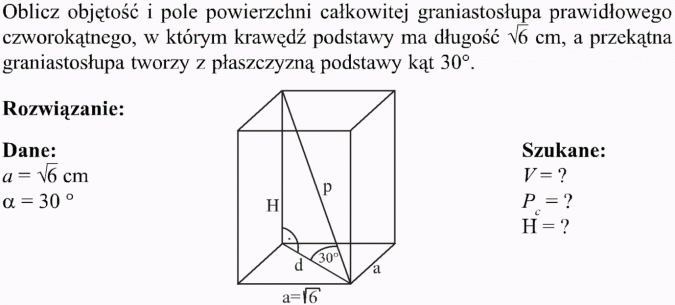
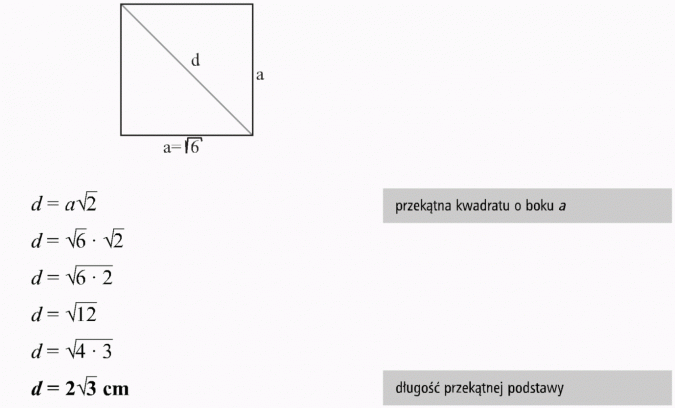
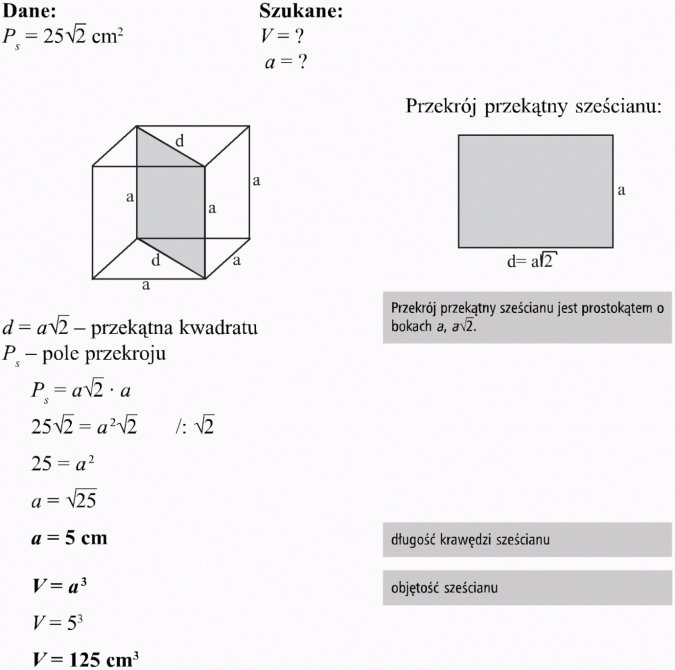
Jeżeli graniastosłup przetniemy płaszczyzną przechodzącą przez dwie krawędzie boczne nie należące do jednej ściany, to otrzymamy czworokąt, który nazywamy przekrojem przekątnym graniastosłupa.
Odp:. Objętość sześcianu wynosi 125 cm3.
Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma 30°. Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.
Rozwiązanie:
Następnie obliczam długość wysokości graniastosłupa. W tym celu wykorzystuję dane dotyczące powierzchni bocznej.
Powierzchnia boczna graniastosłupa po rozwinięciu ma płaszczyznę:
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.