Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Objętość dowolnego ostrosłupa wyraża się wzorem:
Pole powierzchni całkowitej wyraża się wzorem:
Każdą z dwóch części przestrzeni wyznaczonych przez dwie półpłaszczyzny o wspólnej krawędzi l, wraz z tymi półpłaszczyznami, nazywamy kątem dwuściennym.
Miarą kąta dwuściennego nazywamy miarę kąta płaskiego α, będącego wspólną częścią kąta dwuściennego i płaszczyzny prostopadłej do jego krawędzi.
Zapoznajmy się z nazewnictwem niektórych kątów występujących w ostrosłupach.
Przejdźmy teraz do rozwiązania kilku podstawowych i kilku trudniejszych zadań.
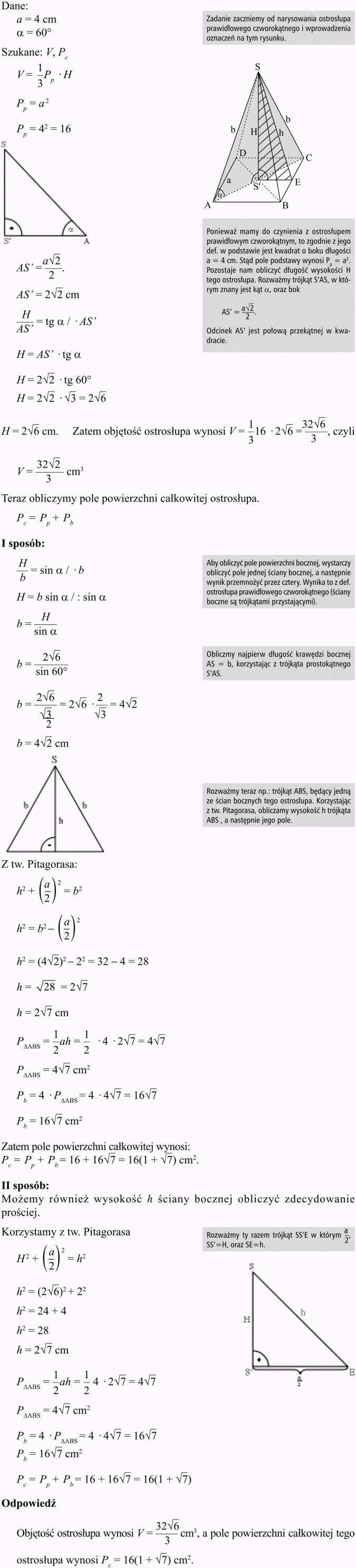
W ostrosłupie czworokątnym prawidłowym krawędź podstawy ma długość a = 4cm. Krawędź boczna tworzy z płaszczyzną podstawy kąt o mierze 60°. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Rozwiązanie:
W ostrosłupie prawidłowym trójkątnym o krawędzi podstawy 6 cm, krawędź boczna tworzy z płaszczyzną podstawy kąt o mierze 45°. Oblicz objętość tego ostrosłupa.
Odpowiedź
Szukana objętość ostrosłupa wynosi V = 18 cm3.
Wyznaczyć objętość prawidłowego ostrosłupa czworokątnego, wiedząc, że pole przekroju ostrosłupa płaszczyzną przechodzącą przez przekątną podstawy i wierzchołek ostrosłupa jest trójkątem równobocznym o polu S.
Pogłębiaj wiedzę w temacie: Objętość i pole powierzchni ostrosłupa
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.