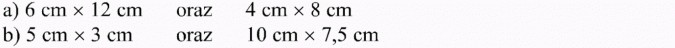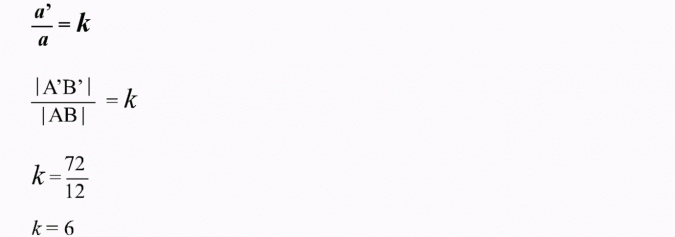Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Figury, mające ten sam kształt, a różniące się co najwyżej wielkością, nazywamy figurami podobnymi.
Dwa prostokąty są podobne, jeżeli stosunek długości dwóch prostopadłych boków jednego prostokąta jest równy stosunkowi długości odpowiednich boków drugiego prostokąta, czyli
Dwa trójkąty prostokątne są podobne, jeżeli stosunek długości przyprostokątnych w jednym trójkącie jest równy stosunkowi długości odpowiednich przyprostokątnych w drugim trójkącie.
Jeżeli dwa trójkąty prostokątne mają po jednym kącie ostrym równym, to te trójkąty są podobne.
Sprawdź, czy prostokąty o podanych bokach są podobne:
Rozwiązanie:
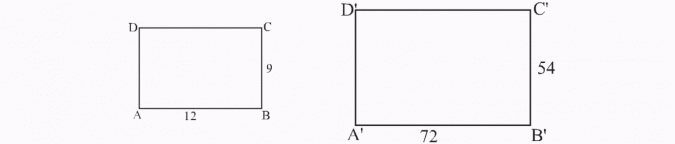
Dany jest prostokąt ABCD, w którym |AB| = 12 cm i |BC|= 9 cm oraz prostokąt A’B’C’D’ o wymiarach |B’C’| = 54 cm i |A’B’| = 72 cm.
Sprawdź, czy prostokąty są podobne. Oblicz skalę podobieństwa.
Rozwiązanie:
Najpierw sprawdzam, czy prostokąty są podobne, czyli czy stosunek długości dwóch prostopadłych boków jednego prostokąta jest równy stosunkowi długości odpowiednich boków drugiego prostokąta.
Teraz obliczam skalę podobieństwa:
Odp.: Skala podobieństwa wynosi 6.
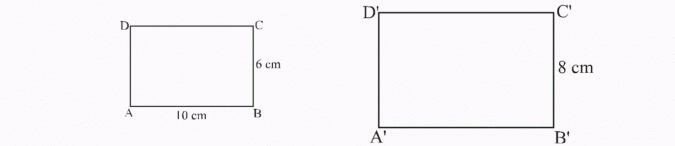
Dane są prostokąty podobne ABCD oraz A’B’C’D’. Długość boku AB = 10cm, |BC| = 6 cm i |B’C’| = 8 cm. Oblicz długość boku A’B’.
Rozwiązanie:
Prostokąty ABCD i A’B’C’D’ są podobne, a zatem:
Ponieważ prostokąty są podobne, to:
Obwód prostokąta ABCD jest równy 20 cm. Oblicz obwód prostokąta A’B’C’D’ podobnego do prostokąta ABCD w skali k = 3,5.
Rozwiązanie:
Odp.: Obwód prostokąta A’B’C’D’ wynosi 70 cm.
Oblicz pole prostokąta A’B’C’D’ podobnego do prostokąta ABCD w skali k = 2, jeżeli |AB| = 5 cm, |BC| = 8 cm.
Rozwiązanie:
Odp.: Pole prostokąta A’B’C’D’ wynosi 160 cm2.
Trójkąt ABC jest podobny do trójkąta A’B’C’. Oblicz długość boku |A’C’|, jeżeli |AB| = 8 cm, |AC| = 5 cm, |A’B’| = 12 cm.
Rozwiązanie:
Odp.: Długość boku |A’C’| wynosi 7,5 cm.
Oblicz obwód trójkąta A’B’C’ podobnego do trójkąta ABC, jeżeli |AB| = 15 cm, |BC| = 8 cm, |AC| = 10 cm, |A’B’| = 5 cm.
Rozwiązanie:
Odp.: Obwód trójkąta A’B’C’ wynosi 11 cm.
Trójkąty ABC i A’B’C’ są podobne. Trójkąt ABC ma boki długości 30 cm, 45 cm i 60 cm. Obwód trójkąta A’B’C’ wynosi 18 cm. Oblicz długości boków trójkąta A’B’C’.
Rozwiązanie:
Obliczam skalę podobieństwa:
Odp.: Długości boków trójkąta A’B’C’ wynoszą 4 cm, 6 cm, 8 cm.
Sprawdzam, czy obwód wynosi 18 cm.
Rozwiązanie:
Gdy Staszek stoi wieczorem 3 m od latarni, to rzuca cień, który ma 1 m. Staszek ma 1,8 m wzrostu. Jaka jest wysokość latarni?
Rozwiązanie:
A zatem z podobieństwa trójkątów wynika:
Odp.: Wysokość latarni wynosi 7,2 m.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.