Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Jeżeli ramiona kąta przetniemy kilkoma prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków na drugim ramieniu kąta.
Wygodnie jest długości odcinków oznaczyć małymi literami.
Z twierdzenie Talesa wynikają też inne ważne proporcje:
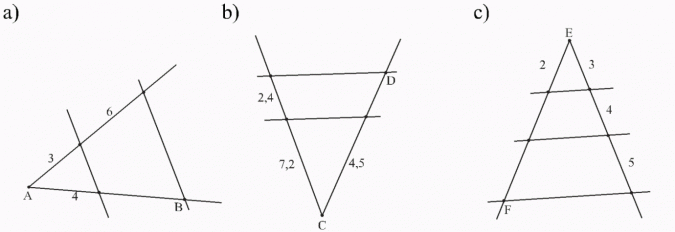
Oblicz długość odcinków AB, CD i EF:
Rozwiązanie:
lub II sposób:
Odp.: Długość odcinka |AB| = 12.
lub II sposób:
Odp.: Długość odcinka |CD| = 6.
Korzystam z twierdzenia Talesa:
Odp.: Długość odcinka |EF| = 8.
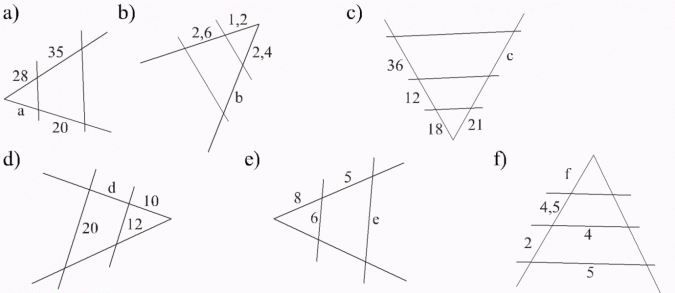
Oblicz długość odcinków zaznaczonych na rysunkach literami:
Rozwiązanie:
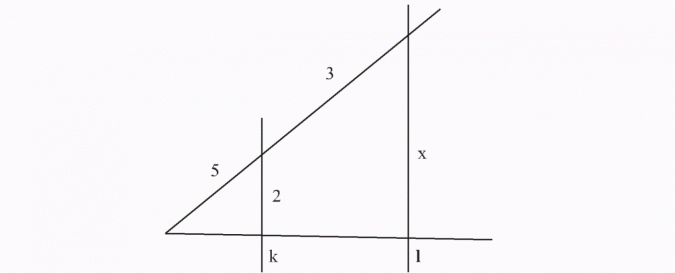
Na rysunku proste k i l są równoległe. Oblicz długość odcinka x.
Rozwiązanie:
Korzystam z twierdzenia Talesa:
Na boku AB trójkąta ABC obrano punkt D taki, że |AD| = 6 cm, |BD| = 0,8 dm. Przez punkt D poprowadzono prostą równoległą do boku BC, która przecina bok AC w punkcie E. Oblicz |AE|, jeżeli |AC| = 280 mm.
Zauważ: ramiona kąta CAB przecięte są prostymi równoległymi (DE || BC), a zatem stosuję twierdzenie Talesa:
Odp.: Odcinek AE ma długość 12 cm.
Oblicz pole zamalowanego trójkąta:
Rozwiązanie:
Z twierdzenia Talesa:
Odp.: Pole trójkąta wynosi 24.
W trapezie ABCD, w którym odcinek AB jest równoległy do odcinka CD, przedłużono boki AD i BC do przecięcia w punkcie O. Oblicz długość odcinka OD wiedząc, że jest on krótszy od odcinka OC o 2cm i |AD| = 28cm, a |BC| = 32cm.
Rozwiązanie:
Ponieważ AB || CD, więc można zastosować twierdzenie Talesa:
Odp.: Odcinek OD ma długość 14 cm.
W trójkącie prostokątnym o przyprostokątnych długości |AC| = 20 cm, |AB| = 16 cm poprowadzono prostą równoległą do boku AB, przecinającą bok AC w punkcie K i bok BC w punkcie L. Odcinek KL ma długość 12cm. Oblicz pole powstałego trapezu ABLK.
Odp.: Pole trapezu wynosi 70cm2.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.