Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
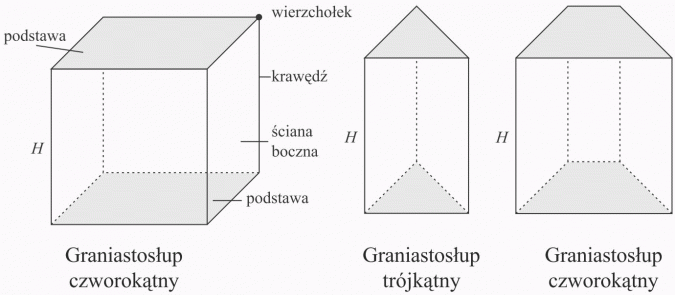
Graniastosłupy mają:
- 2 podstawy, które mogą być dowolnymi wielokątami
- ściany boczne, które są prostokątami
H - to wysokość graniastosłupa
Przyjmujemy oznaczenia:
Pp - pole podstawy
Pb - pole powierzchni bocznej
Pc - pole powierzchni całkowitej
V - objętość graniastosłupa
Jednostki pola: 1 cm2, 1 dm2, 1 m2 ...
Jednostki objętości: 1 cm3, 1 dm3, 1 m3, 1 litr, 1 mililitr ...
Oblicz pole powierzchni i objętość sześcianu o krawędzi 7 dm.
Odpowiedź:
Pole powierzchni sześcianu wynosi 294 dm2, a objętość jest równa 343 dm3.
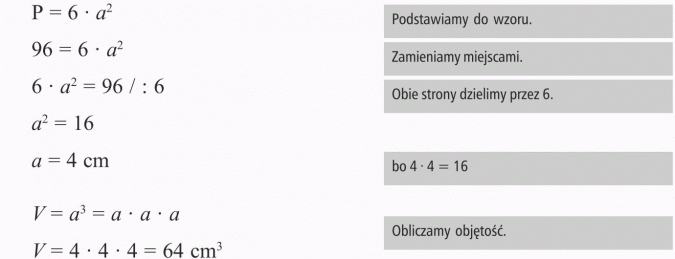
Pole powierzchni sześcianu jest równe 96 cm3. Oblicz objętość.
Odpowiedź:
Objętość wynosi 64 dm3.
Oblicz pole powierzchni i objętość prostopadłościanu o wymiarach 1 m x 6 m x 7 m.
Odpowiedź:
Pole powierzchni sześcianu wynosi 110 dm2, natomiast objętość 42 dm3.
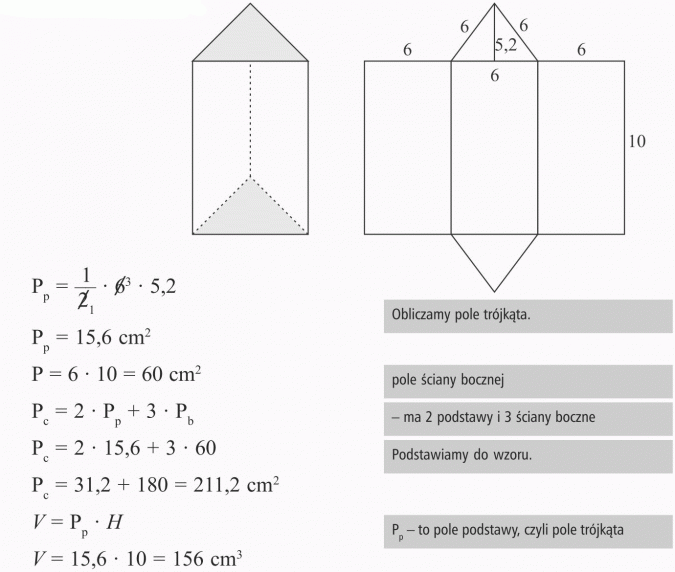
Oblicz pole powierzchni i objętość graniastosłupa trójkątnego, który w podstawie ma trójkąt równoboczny o boku 6 cm i wysokości 5,2; wysokość graniastosłupa wynosi 10 cm.
Odpowiedź:
Pole powierzchni graniastosłupa wynosi 211 dm3, a objętość 156 dm3.
Odpowiedź:
Akwarium wraz z wodą waży 83,5 kg.
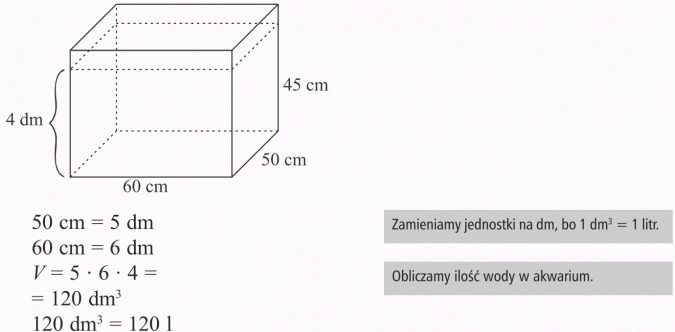
Oblicz, ile litrów wody należy wlać do akwarium o wymiarach podanych na rysunku, aby napełnić je wodą do wysokości 4 dm.
Odpowiedź:
Do akwarium należy wlać 120 l wody.
Krasnoludek chce pomalować prostopadłościenny klocek o wymiarach 1,2 cm, 2 cm, 3 cm. Puszka farby wystarcza na pomalowanie 2,5 cm2 powierzchni. Ile puszek farby powinien kupić krasnoludek?
Odpowiedź:
Krasnoludek musi kupić 10 puszek farby.
Czy z blachy o wymiarach 2 m x 85 cm można sporządzić prostopadłościan o wymiarach 80 cm, 60 cm, 40 cm?
Odpowiedź:
Z blachy nie można sporządzić prostopadłościanu.
1 cm3 srebra waży 10,5 g. Ile ważyłby prostopadłościan o wymiarach 1 dm, 1 dm, 2 dm zrobiony ze srebra?
Odpowiedź:
Srebrny prostopadłościan będzie ważył 21 kg.
3 jednakowe sześciany o krawędzi 1 cm ustawiono dokładnie jeden na drugim. Oblicz pole powstałej bryły.
Odpowiedź:
Pole powstałej bryły wynosi 14 cm2.
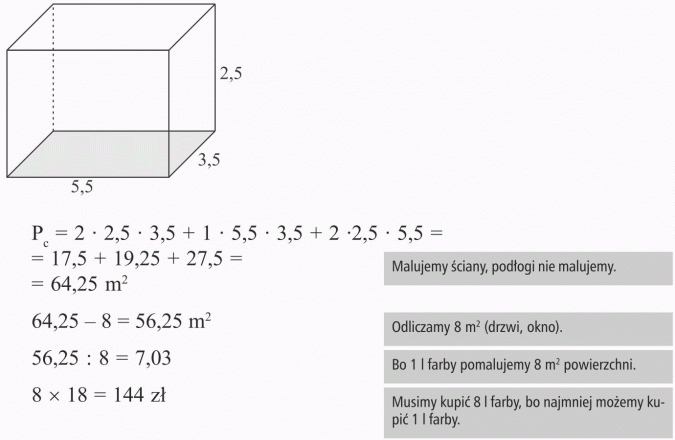
Państwo Kowalscy chcą pomalować pokój o wymiarach 5,5 m x 3,5 m x 2,5 m. Ile zapłacą za farbę, jeżeli 1 litr farby wystarczy na pomalowanie 8 m2 i kosztuje 18 zł? Odliczamy 8 m2, które zajmują okno i drzwi.
Odpowiedź:
Państwo Kowalscy muszą kupić 8 litrów farby i zapłacą 144 zł.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.