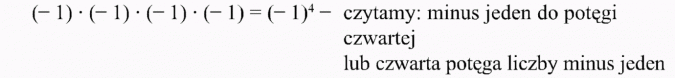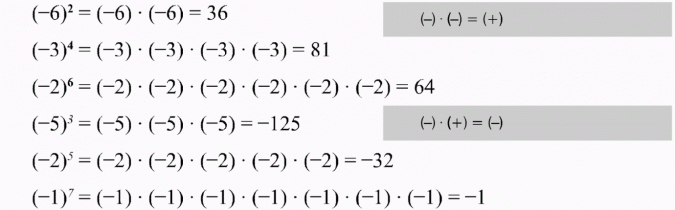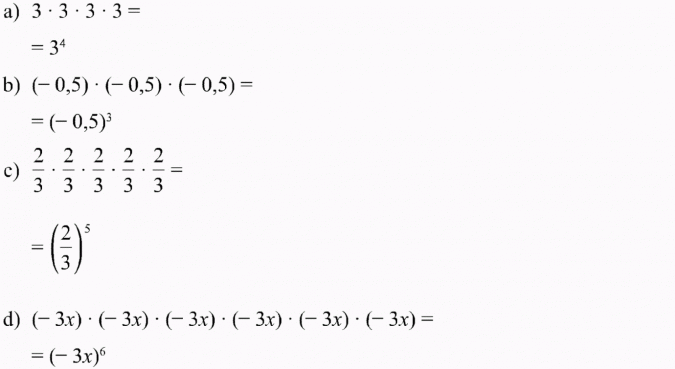Potęga o wykładniku naturalnym

Potęgowanie to skrócony zapis mnożenia jednakowych czynników:

Zamiast pisać: 2 · 2 · 2 · 2 · 2 piszemy: 2⁵ (czytamy dwa do potęgi piątej).

Potęga o wykładniku naturalnym. Wykładnik potęgi. Podstawa potęgi. a jest dowolną liczbą różną od zera.

Uwaga! 0⁰ jest symbolem nieokreślonym (nie oznacza żadnej liczby, nie podnosimy zera do potęgi zerowej).

3 · 3 = 3² - czytamy: kwadrat liczby trzy

3 · 3 = 3² - lub trzy do kwadratu

3 · 3 = 3² - lub druga potęga liczby trzy

3 · 3 = 3² - lub trzy do potęgi drugiej

5 · 5 · 5 = 5³ - czytamy: sześcian liczby pięć

5 · 5 · 5 = 5³ - lub pięć do sześcianu

5 · 5 · 5 = 5³ - lub pięć do potęgi trzeciej

5 · 5 · 5 = 5³ - lub trzecia potęga liczby pięć

Potęga o wykładniku naturalnym. Czytamy: minus jeden do potęgi czwartej lub czwarta potęga liczby minus jeden.

2x · 2x · 2x · 2x · 2x = (2x)⁵ - czytamy: piąta potęga liczby 2x

Przykłady

Potęga o wykładniku naturalnym. Z definicji a^0 = 1.

Potęga liczby nieujemnej jest liczbą nieujemną (liczby nieujemne to liczby dodatnie i liczba 0).

Zauważ, że jeżeli liczbę ujemną podnosimy do potęgi o wykładniku parzystym (tzn. 2, 4, 6, 8, ...), to wynik jest dodatni, jeżeli wykładnik jest nieparzysty, to wynik potęgowania jest ujemny.

Zadanie 1

Zapisz iloczyny w postaci potęgi:

Zadanie 2

Oblicz:

Potęga o wykładniku naturalnym. Liczbę mieszaną zamieniam na ułamek niewłaściwy. Albo: wykładnik jest liczbą parzystą, wynik jest dodatni. Wykładnik jest liczbą nieparzystą, wynik jest ujemny. Wykładnik nieparzysty, wynik ujemny. Wykładnik parzysty, wynik dodatni. Liczbę mieszaną zamieniam na ułamek niewłaściwy.

Zadanie 3

Oblicz:

Potęga o wykładniku naturalnym. Taki zapis (bez nawiasu) oznacza, że tylko licznik należy podnieść do kwadratu. Ten zapis oznacza, że do kwadratu podnosimy ułamek 5/7 i do wyniku dopisujemy znak -. Ten zapis oznacza, że liczbę 6 należy podnieść do kwadratu i do wyniku dopisać znak -. Teraz liczbę (-6) podnosimy do kwadratu. Podnosimy liczbę 0,2 do potęgi czwartej i do wyniku dopisujemy znak -. Wykonujemy tak: 2 x 2 x 2 x 2 = 16 i w liczbie 16 odcinamy 4 miejsca po przecinku, licząc od końca.

Zadanie 4

Oblicz siedem kolejnych potęg liczby 10.

Rozwiązanie

10¹ = 10

10² = 10 · 10 = 100

10³ = 10 · 10 · 10 = 1000

10⁴ = 10 · 10 · 10 · 10 = 10000

10⁵ = 10 · 10 · 10 · 10 · 10 = 100000

10⁶ = 10 · 10 · 10 · 10 · 10 · 10 = 1000000

10⁷ = 10 · 10 · 10 · 10 · 10 · 10 · 10 = 10000000

Czy potrafisz bez obliczania zapisać wartość 10³⁵?

Czy zauważasz związek między wykładnikiem potęgi a liczbą zer w wyniku?

Zadanie 5

Oblicz wartości wyrażeń, pamiętając, że potęgowanie wykonujemy przed mnożeniem i dzieleniem:

Potęga o wykładniku naturalnym. Odejmowanie zastępujemy dodawaniem liczby przeciwnej. Przed wykonaniem mnożenia skracaj. Najpierw potęgowanie. Najpierw potęgujemy. Najpierw dzielenie.

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Potęga o wykładniku naturalnym