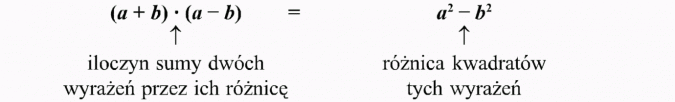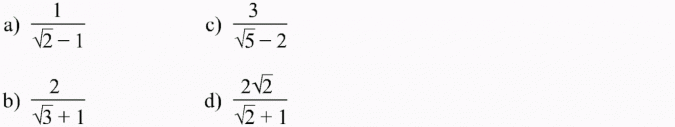Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Kwadrat sumy dwóch wyrażeń:
Kwadrat sumy dwóch wyrażeń równy jest kwadratowi pierwszego wyrażenia plus podwojony iloczyn pierwszego i drugiego wyrażenia plus kwadrat drugiego wyrażenia.
Przykłady
Kwadrat różnicy dwóch wyrażeń:
Kwadrat różnicy dwóch wyrażeń równy jest kwadratowi pierwszego wyrażenia minus podwojony iloczyn pierwszego i drugiego wyrażenia plus kwadrat drugiego wyrażenia.
Przykłady
Różnica kwadratów dwóch wyrażeń
Iloczyn sumy dwóch wyrażeń przez ich różnicę jest równy różnicy kwadratów tych wyrażeń.
Przykłady
Poznane wzory:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(a + b)(a - b) = a2 - b2
nazywają się wzorami skróconego mnożenia
Zapamiętaj je!
Oblicz w pamięci:
Rozwiązanie
Przekształć na iloczyny następujące sumy:
a) x2 + 2xy + y2
b) 4y2 + 8yz + 4z2
c) x2 + 12x + 36
Rozwiązanie
Zamienić sumę na iloczyn, tzn. zapisać ją tak, aby ostatnim działaniem do wykonania było mnożenie. W kl. I pokazałam Ci jeden ze sposobów zamiany sumy na iloczyn. Było to wyłączanie wspólnego czynnika przed nawias. Ale nie zawsze jest to możliwe. Teraz pokażę Ci, jak zamienić sumę na iloczyn, stosując wzory skróconego mnożenia.
Przekształć na iloczyny następujące sumy:
a) x - 2x +1
b) y2 - 10ay + 25a2
c) 49x2 - 56xy + 16y2
Rozwiązanie
Przekształć na iloczyny:
a) x2 - y2
b) 4x2 - 25
c) 100z2 - 25y2
d) 16a2 - 1
Rozwiązanie
Oblicz:
Rozwiązanie
Doprowadź do najprostszej postaci:
a) (x + 4)2 + 4(x - 2)2
b) 3(2 - y)2 + 4(y - 5)2
c) 5(3 - 5a) - 5(3a - 2)(3a +2)
d) (x - 2)(x + 2) - (x - 3)2 + (x + 1)2
Rozwiązanie
Oblicz wartość liczbową wyrażenia:
Rozwiązanie
Ważne
Usuń niewymierność z mianownika:
Rozwiązanie
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.