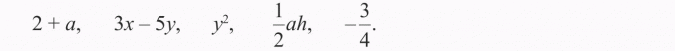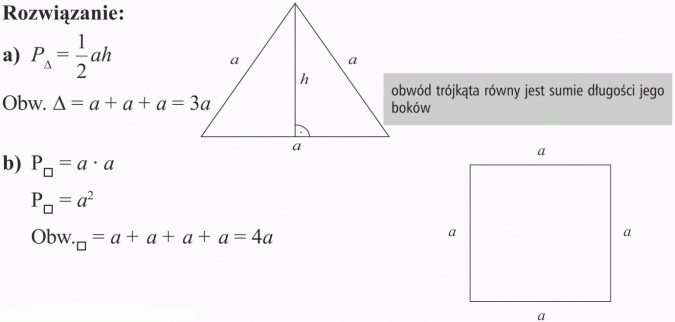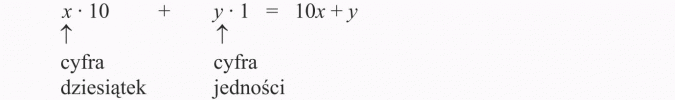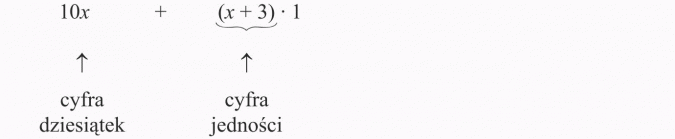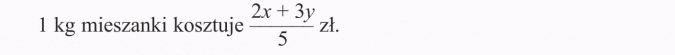Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Wyrażenia, w których występują liczby i litery połączone znakami działań i nawiasami nazywamy wyrażeniami algebraicznymi.
Np.
Uwaga: wyrażenie 3 · x oznacza to samo co 3x (kropkę jako znak mnożenia opuszczamy);
5 · (m + n) oznacza to samo co 5(m + n).
Nazwa wyrażenia algebraicznego pochodzi od ostatniego działania, które należy wykonać zgodnie z kolejnością działań.
Przypomnienie: najpierw wykonujemy działania w nawiasach, potem potęgowanie i pierwiastkowanie, następnie mnożenie i dzielenie, na końcu dodawanie i odejmowanie.
Uwaga: w kółeczkach zaznaczono w jakiej kolejności będziemy wykonywać działania, jeśli za zmienne (litery) podstawimy liczby.
Ułóż i zapisz wyrażenia:
a) suma kwadratu liczby x i podwojonej liczby y.
Rozwiązanie:
Zapiszmy kolejno treść zadania w postaci wyrażeń algebraicznych:
x2 - kwadrat liczby x
2 · y - podwojona liczba y (podwoić tzn. pomnożyć przez 2)
2 · y = 2y (kropkę jako znak mnożenia pomijamy)
Teraz tworzymy sumę tych liczb, tzn. ostatnim działaniem do wykonania powinno być dodawanie, czyli:
x2 + 2y
b) różnica sześcianu liczby a i potrojonej liczby b
Rozwiązanie:
Podobnie jak w punkcie a) zapiszmy treść zadania:
a3 - sześcian liczby a
3b - potrojona liczba b (potroić tzn. pomnożyć przez 3)
Utwórzmy różnicę (czyli odejmowanie) tych wyrażeń:
a3 - 3b
c) iloczyn liczb -2, a i b
Rozwiązanie:
iloczyn, czyli mnożenie, wystarczy pomnożyć:
-2 · a · b, pamiętając, że kropkę jako znak mnożenia pomijamy:
-2ab
d) iloraz kwadratu liczby a przez 3
Rozwiązanie:
e) różnicę kwadratów liczb a i b
Rozwiązanie:
a2 - kwadrat liczby a
b2 - kwadrat liczby b
różnica, czyli odejmowanie, więc zapisujemy:
a2 - b2
Zapisz za pomocą wyrażeń algebraicznych:
a) pole i obwód trójkąta równobocznego o boku a i wysokości h;
b) pole i obwód kwadratu o boku a
Zapisz w postaci wyrażenia algebraicznego:
a) liczbę o 5 większą od x
b) liczbę 5 razy większą od x
c) liczbę o 2 mniejszą od y
d) liczbę 2 razy mniejszą od y
e) połowę liczby a
f) liczbę k pomniejszoną o 10
g) liczbę 4 razy mniejszą od kwadratu liczby n
Rozwiązanie:
a) do liczby x należy dodać 5, czyli
x + 5
b) liczba 5 razy większa oznacza mnożenie przez 5:
5x
c) y - 2 - liczba o 2 mniejsza od y
d) liczba 2 razy mniejsza oznacza dzielnie tej liczby przez 2, a zatem:
Zapisz w postaci wyrażenia algebraicznego:
a) liczbę dwucyfrową, której cyfrą dziesiątek jest x, a cyfrą jedności y;
b) liczbę trzycyfrową, której cyfrą setek jest a, cyfrą dziesiątek b, a cyfrą jedności c;
c) liczbę dwucyfrową, której cyfrą dziesiątek jest x, a cyfra jedności jest o 3 większa od cyfry dziesiątek.
Rozwiązanie:
Zauważ, że liczbę dwucyfrową np. 35 można zapisać:
a) Jeżeli oznaczymy:
x - cyfra dziesiątek
y - cyfra jedności
to liczbę dwucyfrową zapiszemy:
Warto zapamiętać!
10x + y - to ogólny wzór na liczbę dwucyfrową
b) Liczbę trzycyfrową np. 562 można zapisać:
U nas w zadaniu oznaczmy:
a - cyfra setek
b - cyfra dziesiątek
c - cyfra jedności
więc liczbę trzycyfrową zapiszemy:
Warto zapamiętać!
Ogólny wzór na liczbę trzycyfrową 100a + 10b + c
c) x - cyfra dziesiątek
x + 3 - cyfra jedności (o 3 większa od cyfry dziesiątek), więc liczba dwucyfrowa ma postać:
Kasia ma m lat, a Ania jest od niej o 20 lat młodsza. Zapisz wyrażeniem ile lat będą miały razem za 7 lat.
Rozwiązanie:
Oznaczamy:
m - wiek Kasi obecnie
m - 20 - wiek Ani obecnie
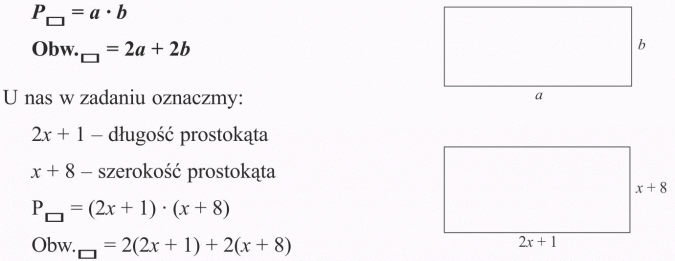
Długość prostokąta wynosi (2x + 1) cm, a szerokość (x + 8) cm. Zapisz:
a) obwód tego prostokąta
b) pole tego prostokąta
Rozwiązanie:
Do rozwiązania zadania potrzebne Ci będą wzory:
Zmieszano 2 kg cukierków po x zł i 3 kg cukierków w cenie y zł za kilogram. Jaka jest cena 1 kg tej mieszanki?
Rozwiązanie:
x - cena 1 kg cukierków I rodzaju
2x - wartość 2 kg cukierków I rodzaju
y - cena 1 kg cukierków II rodzaju
3y - wartość 3 kg cukierków II rodzaju
2x + 3y - wartość całej mieszanki
2 kg + 3 kg = 5 kg - waga całej mieszanki
więc 1 kg tej mieszanki kosztuje:
(2x + 3y) : 5
Odp.:
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.