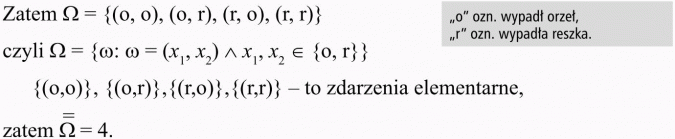Algebra zdarzeń

Przestrzenią zdarzeń elementarnych (przestrzenią wyników) nazywamy zbiór wszystkich możliwych wyników doświadczenia losowego.

Zdarzeniem elementarnym nazywamy każdy jednoelementowy podzbiór przestrzeni wyników.

Zdarzeniem (zdarzeniem losowym) nazywamy każdy podzbiór przestrzeni wyników.

W rachunku prawdopodobieństwa stosujemy następujące oznaczenia i określenia:

Algebra zdarzeń. Omega - litera alfabetu greckiego. Przestrzeń wyników, zdarzenia elementarne, zdarzenie losowe, zdarzenie niemożliwe, zdarzenie pewne, zdarzenie przeciwne do zdarzenia, suma zdarzeń, iloczyn zdarzeń, różnica zdarzeń, zdarzenia wykluczają się, zdarzenia są identyczne, zdarzenie pociąga za sobą zdarzenie (zdarzenie zawiera się w zdarzeniu), zdarzenie elementarne sprzyja zdarzeniu, moc (liczba elementów) zbioru tzn. liczba zdarzeń elementarnych sprzyjających zdarzeniu, moc zbioru tzn. liczba wszystkich zdarzeń elementarnych w danym doświadczeniu. Zdarzeniem przeciwnym do A nazywamy zbiór wszystkich zdarzeń elementarnych przestrzeni omega, które nie sprzyjają zdarzeniu A. Sumą zdarzeń A i B nazywamy zbiór wszystkich zdarzeń elementarnych przestrzeni omega, które sprzyjają co najmniej jednemu ze zdarzeń A, B. Iloczynem zdarzeń A i B nazywamy zbiór wszystkich zdarzeń elementarnych przestrzeni omega, które sprzyjają zdarzeniu A i zdarzeniu B. Różnicą zdarzeń A i B nazywamy zbiór wszystkich zdarzeń elementarnych przestrzeni omega, które sprzyjają zdarzeniu A i nie sprzyjają zdarzeniu B.

Przykład 1

Doświadczenie polega na dwukrotnym rzucie monetą.

Algebra zdarzeń. Zdarzenie elemtarne. Wypadł orzeł, wypadła reszka.

Niech A będzie zdarzeniem polegającym na tym, że przynajmniej raz wypadnie orzeł, a zdarzenie B - wyniki obu rzutów będą takie same.

Zdarzeniu A sprzyjają zdarzenia elementarne: {(o, o)}, {(o, r)}, {(r, o)}, co możemy zapisać:

Algebra zdarzeń. A' - zdarzenie przeciwne do A polega na tym, że orzeł nie wypadnie ani razu. Zatem sprzyjającym zdarzeniu A' jest zdarzenie elementarne {(r, r)}. B' - polega na tym, że wyniki obu rzutów są różne.

Zadanie 1

Określ zbiór wszystkich możliwych wyników oraz jego moc w następujących doświadczeniach losowych:

a) losujemy z urny jedną z dziesięciu ponumerowanych kul,

b) losuj emy bez zwracania dwie kule spośród pięciu, ponumerowanych od 1 do 5,

c) losujemy kolejno cztery kule spośród 10 ponumerowanych liczbami od 1 do 10, zwracając je za każdym razem po zapisaniu ich numeru,

d) losujemy bez zwracania 3 karty z talii liczącej 52 karty,

e) ustawiamy 8 osób w szeregu.

Rozwiązanie:

Algebra zdarzeń. Przestrzeń wyników jest zbiorem liczb naturalnych od 1 do 10 włącznie. Przestrzeń wyników jest zbiorem par... Zdarzenia elementarne są tutaj zatem dwuwyrazowymi wariacjami bez powtórzeń zbioru {1, 2, 3, 4, 5}. Zdarzeniami elementarnymi w tym doświadczeniu są 4-elementowe ciągi postaci (a, b, c, d), gdzie a, b, c, d e należą do {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} - wyrazy ciągu mogą się powtarzać i są to numery kul wylosowanych odpowiednio: za pierwszym, drugim, trzecim i czwartym razem, czyli... Zatem mamy do czynienia z 4-wyrazowymi wariacjami z powtórzeniami zbioru 10-elementowego. Zdarzeniami elementarnymi są tutaj 3-elementowe podzbiory zbioru 52 kart. K - zbiór stanowiący talię kart. Mamy zatem do czynienia z 3-wyrazowymi kombinacjami zbioru 52-elementowego. Licznik i mianownik skracamy przez 49!

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Algebra zdarzeń