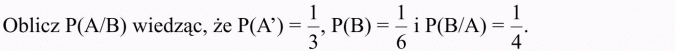Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
W wielu przypadkach, informacja o zajściu zdarzenia B ma pewien wpływ na wartość obliczanego prawdopodobieństwa zdarzenia A.
Z liczb 1, 2, 3, 4, 5 losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo:
a) zdarzenia A polegającego na tym, że iloczyn wylosowanych liczb jest większy od 10,
b) zdarzenia B polegającego na tym, że za pierwszym razem wylosowano liczbę nieparzystą,
c) zdarzenia C polegającego na tym, że iloczyn wylosowanych liczb jest większy niż 10 i że za pierwszym razem wylosowano liczbę nieparzystą,
d) zdarzenia D polegającego na tym, że iloczyn wylosowanych liczb jest większy niż 10 jeśli wiadomo, że za pierwszym razem wylosowano liczbę nieparzystą.
Rozwiązanie:
Zapamiętaj!
Zdarzenie polegające na zajściu zdarzenia A, przy założeniu, że zaszło zdarzenie B, oznaczamy symbolem A/B, prawdopodobieństwo tego zdarzenia P(A/B) nazywamy prawdopodobieństwem warunkowym.
Uwaga!
W modelu klasycznym, tzn. gdy wszystkie możliwe wyniki są jednakowo prawdopodobne, prawdopodobieństwo warunkowe można obliczyć ze wzoru:
Wniosek:
Rozwiązanie:
Z definicji prawdopodobieństwa warunkowego mamy:
Rozwiązanie:
Z definicji prawdopodobieństwa warunkowego mamy:
Z talii kart losujemy jedną kartę. Jakiejest prawdopodobieństwo, że będzie ona figurą (asem, królem, damą waletem), jeśli wiadomo, że jest koloru pik?
Rozwiązanie:
Doświadczenie polega na losowaniu jednej karty spośród 52. Zdarzeniami elementarnymi są jednoelementowe kombinacje zbioru 52 kart, czyli:
Z talii 52 kart losujemy dwie karty. Jakie jest prawdopodobieństwo, że przynajmniej jedna z nich będzie starsza od 9, pod warunkiem, że żadna z wylosowanych kart nie jest karem?
Rozwiązanie:
Doświadczenie polega na jednoczesnym losowaniu dwóch kart spośród 52. Zdarzeniami elementarnymi są dwuelementowe kombinacje zbioru 52 kart, czyli:
Rzucamy dwiema symetrycznymi kostkami do gry. Jakie jest prawdopodobieństwo, że suma wyrzuconych oczek będzie równa 6, jeśli wiadomo, że na co najmniej jednej kostce wypadnie liczba pierwsza?
Rozwiązanie:
Z grupy 4 mężczyzn i 3 kobiet wybrane zostaną losowo 2 osoby. Jakie jest prawdopodobieństwo, że obie wylosowane osoby będą kobietami?
Rozwiązanie:
Oznaczmy następująco zdarzenia:
W pudełku znajdują się 52 klocki, z których 13 jest koloru zielonego. Rozdajemy kolejno każdemu z czwórki dzieci po 13 klocków. Jakie jest prawdopodobieństwo, że pierwsze dziecko otrzyma 6 zielonych klocków, drugie 4 zielone klocki, trzecie dziecko 1 zielony, a czwarte 2 w kolorze zielonym?
Rozwiązanie:
Oznaczmy następująco zdarzenia:
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.