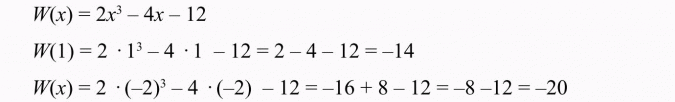Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Twierdzenie
Dwa wielomiany są równe, wtedy i tylko wtedy, gdy są tego samego stopnia i mają równe współczynniki przy odpowiednich potęgach zmiennej.
Oblicz wartości W(1), W(-2) dla wielomianu postaci W(x) = 2x3 - 4x - 12.
Rozwiązanie:
Wyznacz współczynniki a, b, c, wiedząc, że W(x) = x5 + ax2 + bx + c, W(-1) = 1, W(0) = 1, W(1) = -1.
Rozwiązanie:
Skoro dla wielomianu W(x) zachodzą warunki: W(-1) = 1, W(0) = 1, W(1) = -1, to możemy zapisać następujący układ równań:
Odpowiedź
Szukany wielomian ma postać W(x) = x5 - x2 - 2x + 1.
Wyznacz wartości parametrów a, b, c tak, aby wielomiany: W(x) = (a + 1)x3 + 3x2 - 5cx - 2, P(x) = 2x3 + bx2 - 12x - 2 były równe.
Rozwiązanie:
Porównujemy współczynniki przy odpowiednich potęgach obu wielomianów.
Odpowiedź
Wielomiany W(x) i P(x) są równe dla a = 1, b = 3, c = 2,4.
Pierwiastkiem wielomianu W(x) nazywamy jego miejsce zerowe, to znaczy taką liczbę r, że W(r) = 0.
Twierdzenie
Reszta z dzielenia wielomianu W(x) przez dwumian (x - r) jest równa W(r).
Ważnym twierdzeniem jest tak zwane twierdzenie Bézouta.
Twierdzenie Bézouta
Liczba r jest pierwiastkiem wielomianu W(x) wtedy i tylko wtedy, gdy wielomian W(x) dzieli się przez (x - r) bez reszty.
Sprawdź, czy liczba r = 0,5 jest pierwiastkiem wielomianu:
W(x) = 2x4 + x3 + 5x2 - 2x - 0,5.
Rozwiązanie:
Aby sprawdzić, czy liczba r = 0,5 jest pierwiastkiem wielomianu W(x), należy skorzystać z definicji pierwiastka, czyli sprawdzić równość W(r) = 0. Zatem obliczamy wartość wielomianu dla r = 0,5:
Odpowiedź
Liczba r = 0,5 jest pierwiastkiem wielomianu.
Sprawdź, które liczby {3, -2, 1, -1, 0} są pierwiastkami wielomianu W(x) = 2x4 + x3 - x2 - 2.
Rozwiązanie:
Zgodnie z definicją pierwiastka wielomianu wystarczy sprawdzić czy wartość wielomianu dla tych liczb wynosi zero.
Widzimy, że po obliczeniu wszystkich wartości spośród wymienionych liczb wielomian ma jeden pierwiastek.
Wyznacz wartość parametru a tak, aby liczba r = 2 była pierwiastkiem wielomianu W(x) = x5 + x3 + ax2 - 8.
Rozwiązanie
Odpowiedź
Dla a = -8 pierwiastkiem wielomianu W(x) jest liczba 2.
Twierdzenie:
Każdy wielomian o współczynnikach rzeczywistych można rozłożyć na czynniki liniowe lub nierozkładalne czynniki stopnia drugiego (Δ < 0).
Uwaga!
Jak znajdować szybko wymierne pierwiastki wielomianu? Jak dzielić wielomian przez dwumian, nie stosując dzielenia pisemnego? Na te pytania odpowiemy sobie już za chwilę. Poznajmy metodę dzielenia wielomianu przez dwumian, stosując tak zwaną tabelkę Hornera.
Omówmy tę metodę na przykładzie. Mamy podzielić wielomian.
Zgodnie z tematem zadania mamy wielomian postaci:
Wielomian jest stopnia trzeciego, zatem tabelka będzie wyglądać następująco:
Omówimy na tym przykładzie, jak uzupełnia się tabelę Hornera, krok po kroku.
W pierwszym wierszu wpisujemy wszystkie stopnie wielomianu, w drugim wierszu natomiast wszystkie współczynniki tego wielomianu. Współczynnik przy najwyższej potędze zawsze przepisujemy w trzecim wierszu w tej samej kolumnie. Przystępujemy do obliczeń. Mnożymy liczbę z kolumny III przez r = 1 i dodajemy do tego liczbę z kolumny II (u nas 1 · 3 + 2 = 5). Wynik 5 wpisujemy w II kolumnie, w trzecim wierszu. Następnie mnożymy tę liczbę 5 przez r = 1 i dodajemy liczbę z I kolumny (u nas 5 · 1 + (-4) = 1). Wynik tego działania wpisujemy do kolumny I, do wiersza trzeciego. Jeszcze raz postępujemy analogicznie, czyli liczbę 1 mnożymy przez r = 1 i dodajemy liczbę z kolumny 0 (u nas 1 · 1 + 5 = 6). Wynik wpisujemy do kolumny 0, w wiersz trzeci. Na koniec wszystko odkreślamy, przepisując ostatni wiersz jako wiersz czwarty, przesuwając jednocześnie wszystko o jedno miejsce w prawo. To, co nam zostanie po prawej stronie tabeli, jest resztą z dzielenia. Patrz tabelka!!!
W wyniku dzielenia wielomianu W(x) = 3x3 + 2x2 - 4x + 5 przez dwumian (x - 1) otrzymujemy wielomian Q(x) = 3x2 + 5x2 + 1, i resztę R(x) = 6.
Możemy teraz zapisać wielomian w postaci: W(x) = Q(x)(x - 1) + R(x), czyli
Wykonaj dzielenie wielomianu W(x) przez dwumian P(x), stosując tabelkę Hornera.
Liczby 1 i 2 są pierwiastkami wielomianu W(x). Znajdź współczynniki a, b tego wielomianu W(x) = x3 + ax2 - bx + 6.
Rozwiązanie
W ten sposób otrzymujemy układ równań z dwiema niewiadomymi, który następnie rozwiązujemy.
Odpowiedź:
Szukany wielomian ma postać W(x) = x3 - 7x + 6.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.