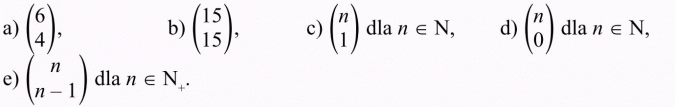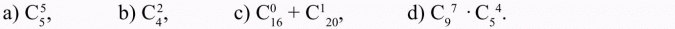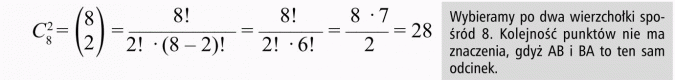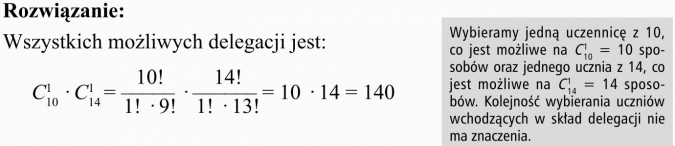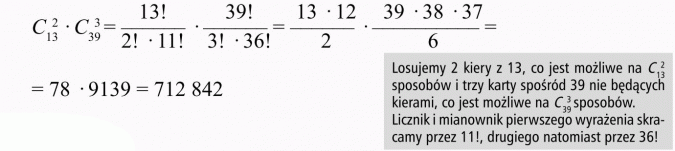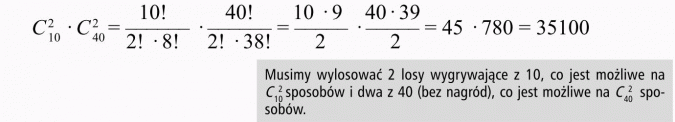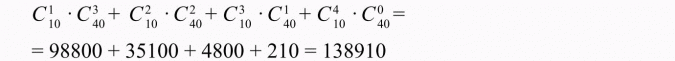Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Zapamiętaj!
Oblicz:
Rozwiązanie:
Odpowiedź
Zapamiętaj!
Z k-elementowymi kombinacjami n-elementowego zbioru mamy do czynienia wtedy, gdy z elementów danego zbioru wybieramy po k elementów bez zwracania i tworzymy z nich zbiór (nie ciąg), tzn. kolejność elementów nie ma znaczenia.
W urnie znajdują się 4 kule: biała, czarna, niebieska i zielona. Losujemy bez zwracania 2 kule. Ile możemy otrzymać różnych wyników losowania?
Rozwiązanie:
Kolejność wylosowanych kul nie ma znaczenia.
Zatem do zapisywania wyniku takiego losowania nie możemy zastosować ciągów. Wyniki losowania traktujemy jako 2-elementowe podzbiory zbioru {b, c, n, z}. Wypiszmy zatem wszystkie możliwe:
{b, c}, {b, n}, {b, z}, {c, n}, {c, z}, {n, z}.
Odpowiedź
Losowanie opisane w zadaniu może zakończyć się 6 różnymi wynikami.
W urnie znajduje się 20 kul ponumerowanych od 1 do 20. Losujemy bez zwracania 3 kule. Ile jest możliwości wylosowania wszystkich 3 kul o numerze, będącym liczbą parzystą?
Rozwiązanie:
Wśród liczb od 1 do 20 jest 10 parzystych.
Gdyby kolejność wylosowanych kul była ważna, wszystkich możliwych wyników losowania byłoby:
Odpowiedź
Wszystkich możliwości wylosowania 3 kul o numerach będących liczbami parzystymi spośród kul ponumerowanych od 1 do 20 jest 120.
Oblicz;
Rozwiązanie:
Ile jest wszystkich odcinków łączących wierzchołki ośmiokąta wypukłego?
Rozwiązanie:
Są to 2-elementowe kombinacje zbioru 8-elementowego i jest ich:
Odpowiedź
Wszystkich odcinków jest 28.
W klasie jest 24 uczniów, w tym 10 dziewcząt. Na ile sposobów można wybrać 2-osobową delegację złożoną z uczennicy i ucznia?
Odpowiedź
Delegację tej klasy złożoną z uczennicy i ucznia można wybrać na 140 sposobów.
Ile nastąpi uścisków dłoni, gdy spotka się 10-osobowa grupa znajomych, zakładając, że wita się każdy z każdym?
Rozwiązanie:
Są to 2-elementowe kombinacje zbioru 10-elementowego i jest ich:
Odpowiedź
Przy powitaniu nastąpi 45 uścisków dłoni.
Z talii liczącej 52 karty losujemy bez zwracania pięć kart. Ile istnieje możliwych wyników losowania, w których otrzymamy dokładnie dwa kiery?
Rozwiązanie:
W talii 52 kart są 4 kolory (trefl, karo, kier, pik) po 13 kart w każdym. Kolejność wylosowanych kart nie ma znaczenia. Zatem wszystkich możliwości mamy:
Odpowiedź
Możliwych wyników losowania 5 kart z talii, tak aby 2 z nich były kierami jest 712 842.
W urnie znajduje się 10 kul białych i 6 czarnych. Losujemy bez zwracania 4 kule. Ile jest możliwych wyników losowania, w których dokładnie trzy kule będą tego samego koloru?
Rozwiązanie:
Możliwe są dwa przypadki: trzy kule będą białe i jedna czarna lub trzy czarne i jedna biała.
W pierwszym przypadku możliwości mamy:
Odpowiedź
Wszystkich sposobów wylosowania czterech kul, wśród których trzy będą jednego koloru, jest w tym przypadku 920.
Spośród 50 losów pewnej loterii fantowej tylko 10 jest wygrywających. Na ile sposobów można wybrać 4 losy tak, aby co najmniej jeden z nich był wygrywający?
Rozwiązanie:
Co najmniej jeden z czterech możliwych tzn. jeden, dwa, trzy lub cztery. Rozpatrzmy 4 przypadki:
a) jeden z 4 wylosowanych losów jest wygrywający, wówczas możliwości mamy:
b) dwa z 4 wylosowanych losów są wygrywające, wówczas możliwości mamy:
b) trzy z 4 wylosowanych losów są wygrywające, wówczas możliwości mamy:
b) wszystkie 4 wylosowane losy są wygrywające, wówczas możliwości mamy:
Podsumujmy liczbę możliwości wynikającą z wszystkich przypadków:
Odpowiedź
Wszystkich sposobów wylosowania 4 losów w tej loterii tak, aby co najmniej jeden z nich był wygrywający, jest 138 910.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.