Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Zapamiętaj!
Z k-wyrazowymi wariacjami z powtórzeniami danego zbioru mamy do czynienia wtedy, gdy k razy wybieramy po jednym elemencie ze zwracaniem z tego zbioru.
Ile różnych wyników możemy otrzymać rzucając trzy razy monetą?
Rozwiązanie:
Wynikiem rzutu monetą może być orzeł (ozn. o) lub reszka (ozn. r).
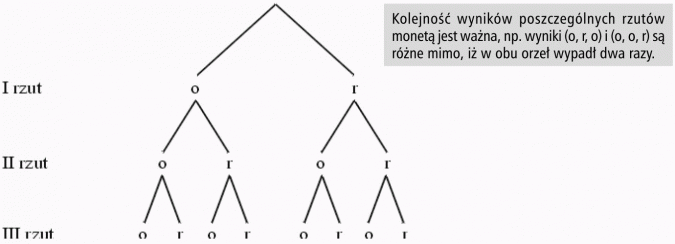
Przedstawmy możliwe wyniki za pomocą drzewka:
Otrzymane wyniki możemy zapisać w postaci następujących ciągów:
(o, o, o,), (o, o, r), (o, r, o), (o, r, r), (r, o, o,), (r, o, r), (r, r, o), (r, r, r).
Są to 3-wyrazowe wariacje z powtórzeniami zbioru dwuelementowego i jest ich wszystkich 8.
Odpowiedź
Wszystkich możliwych wyników trzykrotnego rzutu monetą jest 8.
Na ile różnych sposobów mogą 4 osoby wsiąść do tramwaju złożonego z dwóch wagonów?
Rozwiązanie:
Dla ułatwienia ponumerujmy wagony liczbami 1 i 2 oraz nazwijmy pasażerów jako osoby A, B, C i D. Każdemu pasażerowi przyporządkujmy numer wagonu, do którego wsiądzie. Jednym z możliwych przypadków jest:
| Pasażer | A | B | C | D |
| Nr wagonu | 1 | 1 | 2 | 2 |
Elementy zbioru {1, 2} powtarzają się, kolejność ich jest ważna, zatem mamy do czynienia z 4-wyrazowymi wariacjami z powtórzeniami zbioru 2-elementowego. Każdy z czterech pasażerów ma 2 możliwości dokonania wyboru wagonu, zatem wszystkich sposobów jest:
2 · 2 · 2 · 2 = 24 = 16
Odpowiedź
Wszystkich możliwości rozmieszczenia pasażerów w tym tramwaju jest 16.
Na ile różnych sposobów można włożyć pięć różnych przedmiotów do trzech szuflad?
Rozwiązanie:
Odpowiedź
Pięć różnych przedmiotów można umieścić w trzech szufladach na 243 różne sposoby.
Do windy w dziesięciopiętrowym budynku, stojącej na parterze, wsiadło 6 osób.
Na ile sposobów mogą one wysiąść z windy na poszczególnych piętrach?
Rozwiązanie:
Każda z 6 osób wysiada na jednym z dziesięciu pięter. Aby rozróżnić osoby, oznaczmy je kolejnymi literami alfabetu. Jednymi z wielu możliwości są sytuacje:
| Osoba | A | B | C | D | E | F |
| Nr piętra | I | II | VI | III | III | IX |
| Osoba | A | B | C | D | E | F |
| Nr piętra | III | I | II | VI | IX | III |
W obydwu sytuacjach na III piętrze wysiadły dwie osoby, na I, II, VI i IX po jednej, a na IV, V, VII, VIII i X nie wysiadł nikt. Jednak są to różne dwa sposoby opuszczenia windy przez pasażerów - te same osoby w obu przypadkach wysiadły na innych piętrach. Sytuacje opisane w tabelkach możemy przedstawić w postaci ciągów: (I, II, VI, III, III, IX) oraz (III, I, II, VI, IX, III), gdzie wyrazami ciągów są numery pięter, na których wysiadły poszczególne osoby w kolejności alfabetycznej. Wszystkich możliwych takich ciągów jest:
Sześciu pasażerów może wysiąść z windy dziesięciopiętrowego budynku na 1 000 000 różnych sposobów.
W urnie znajduje się 8 ponumerowanych kul od 1 do 8. Losujemy kolejno 3 kule, zwracając je za każdym razem do urny po zapisaniu ich numerów. Ile liczb trzycyfrowych możemy w ten sposób otrzymać?
Rozwiązanie:
Przyjmijmy, że numer pierwszej wylosowanej kuli jest cyfrą setek, drugiej cyfrą dziesiątek, trzeciej kuli cyfrą jedności.
Zatem w tym przypadku wszystkich możliwości utworzenia liczb jest:
Wszystkich możliwych liczb spełniających warunki zadania jest 512.
Ile różnych wyników możemy otrzymać przy:
a) sześciokrotnym rzucie monetą,
b) rzucie sześcioma monetami o różnych nominałach?
Rozwiązanie:
Ad a)
Rzucając monetą możemy otrzymać dwa wyniki:
- wypadł orzeł - wynik oznaczmy „o”,
- wypadła reszka - wynik oznaczmy „r”.
Zapisując kolejno wyniki poszczególnych rzutów, utworzymy 6-wyrazowe ciągi o wyrazach ze zbioru {o, r}, np.(o, r, o, r, r, o), (r, r, r, r, r, r), itp.
Wszystkich możliwych wyników otrzymamy:
Rzucając sześciokrotnie monetą możemy otrzymać 64 różne wyniki.
Ad b)
Wynik: „o” lub „r”, otrzymany w rzucie każdą z sześciu monet zapisujemy zawsze w tej samej kolejności (np. jako pierwszy zapisujemy wynik rzutu monetą o najmniejszym nominale, potem kolejno o co raz większym nominale, na końcu wynik rzutu monetą o największym nominale). Zatem tworzymy ciągi, których wyrazy mogą się powtarzać i ich kolejność jest ważna. Wszystkich możliwości mamy więc tyle samo, ile w poprzednim przypadku.
Rzucając sześcioma monetami o różnych nominałach możemy otrzymać tyle samo różnych wyników, ile w przypadku sześciokrotnego rzutu monetą, tj. 64.
Rzucamy cztery razy kostką do gry, zapisując liczbę oczek uzyskanych w kolejnych rzutach. Ile różnych liczb czterocyfrowych możemy w ten sposób otrzymać?
Rozwiązanie:
Różnych liczb czterocyfrowych możemy otrzymać 1296.
Ile różnych sześciocyfrowych numerów telefonów może zaproponować centrala swoim abonentom?
Rozwiązanie:
Wszystkich możliwych numerów sześciocyfrowych jest tyle, ile 6-wyrazowych wariacji z powtórzeniami zbioru 10-elementowego.
Zauważmy, że nie możemy jednak brać pod uwagę numerów zaczynających się na „0”. Zastanówmy się, ile ich jest.
Jeśli „0” jest pierwszą wylosowaną cyfrą, to pozostałe pięć cyfr możemy wylosować na tyle sposobów, ile jest 5-wyrazowych wariacji z powtórzeniami zbioru 10-elementowego, czyli
Odpowiedź
Wszystkich mozliwych sześciocyfrowych numerów telefonicznych jest 900 000.
Ile można utworzyć wszystkich parzystych liczb pięciocyfrowych?
Odpowiedź
Wszystkich parzystych liczb pięciocyfrowych jest 45000.
Ile istnieje ciągów co najwyżej 7-wyrazowych utworzonych z elementów zbioru {a, b}?
Rozwiązanie:
Ciągi mają być co najwyżej 7-wyrazowe, czyli mogą być 1-wyrazowe, 2-wyrazowe, 3-wyrazowe itd. aż do 7-wyrazowych włącznie. W każdym przypadku są to wariacje z powtórzeniami zbioru 2-elementowego.
Odpowiedź
Wszystkich co najwyżej 7-elementowych ciągów, utworzonych z elementów zbioru {a, b} jest 254.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.