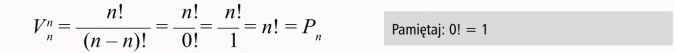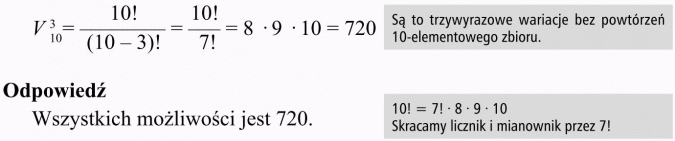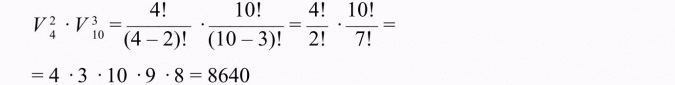Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Zapamiętaj!
Z k-wyrazowymi wariacjami bez powtórzeń danego zbioru mamy do czynienia wtedy, gdy k razy wybieramy bez zwracania po jednym elemencie z tego zbioru.
Dany jest zbiór X = {1, 2, 3}. Wypisz wszystkie możliwe liczby dwucyfrowe o różnych cyfrach, jakie można utworzyć z elementów zbioru X. Ile jest wszystkich możliwości?
Rozwiązanie:
Liczby dwucyfrowe to dwuelementowe ciągi, czyli dwuwyrazowe wariacje bez powtórzeń (cyfry mają być różne) zbioru 3-elementowego.
Cyfrę dziesiątek możemy zapisać na 3 sposoby: cyfra 1, 2 lub 3, cyfrę jedności natomiast już tylko na 2 sposoby (jeśli wybierzemy cyfrę dziesiątek, zostaną do wyboru dwie cyfry). Zatem wszystkich możliwości jest:
2 · 3 = 6
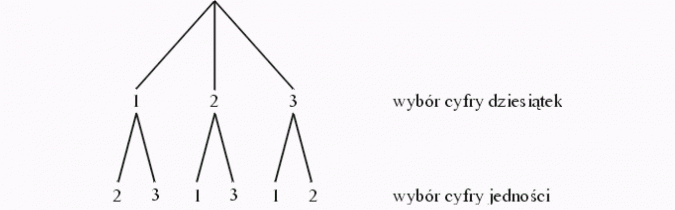
Aby wypisać wszystkie możliwości, możemy posłużyć się grafem zwanym drzewem kombinatorycznym:
Zatem są to liczby: 12, 13, 21, 23, 31, 32.
Odpowiedź
Wszystkich możliwości jest 6.
Szyfr do sejfu składa się z czterech różnych cyfr od 1 do 9 włącznie. Ile jest wszystkich możliwości, jeżeli pierwsza cyfra jest większa od 6?
Odpowiedź
Wszystkich możliwych szyfrów spełniających warunki zadania jest 1008.
Z urny, w której znajduje się 9 ponumerowanych kul od 1 do 9 włącznie, losujemy kolejno bez zwracania 3 kule. Zapisując wyniki losowań tworzymy liczby trzycyfrowe. Ile można utworzyć w ten sposób liczb mniejszych od 780?
Rozwiązanie:
Pierwszą cyfrą (cyfrą setek) może być każda cyfra od 1 do 7 włącznie (8 i 9 nie może, bo liczba ma być mniejsza od 780). Rozważmy dwa przypadki:
a) cyfrą setek jest 7,
b) cyfra setek jest elementem zbioru {1, 2, 3, 4, 5, 6}.
Odpowiedź
Wszystkich liczb trzycyfrowych spełniających warunki zadania jest 378.
Przykład
Uwaga!
Gdy n = k, to wariacje bez powtórzeń są permutacjami:
W finale konkursu matematycznego bierze udział 10 uczestników. Ile jest możliwości zajęcia przez nich trzech pierwszych miejsc, jeżeli uwzględniamy kolejność (I, II i III miejsce)?
Rozwiązanie:
Ile jest wszystkich liczb pięciocyfrowych o różnych cyfrach, podzielnych przez 5?
Rozwiązanie:
Liczba jest podzielna przez 5, jeśli jej cyfrą jedności jest 0 lub 5.
Zatem rozpatrzmy dwa przypadki:
a) cyfrą jedności jest 0,
b) cyfrą jedności jest 5.
Odpowiedź
Wszystkich liczb pięciocyfrowych o różnych cyfrach, podzielnych przez 5, jest 5712.
W pewnej fabryce postanowiono wprowadzić identyfikatory dla pracowników w niej zatrudnionych. Numer każdego identyfikatora ma być inny. Składać ma się on w kolejności: najpierw z dwóch różnych liter ze zbioru {A, B, C, D}, a następnie z trzech różnych cyfr spośród wszystkich możliwych (zero może stanowić pierwszą z trzech cyfr). Czy każdy pracownik tej fabryki otrzymałby identyfikator, gdyby liczba wszystkich zatrudnionych wynosiła 8600?
Rozwiązanie:
Numer identyfikatora potraktujemy jako pięciowyrazowy ciąg:
Zatem wszystkich możliwych numerów identyfikatora w tej fabryce jest:
Odpowiedź
W przypadku zatrudnienia 8600 pracowników, wszyscy zatrudnieni dostaną identyfikatory.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.