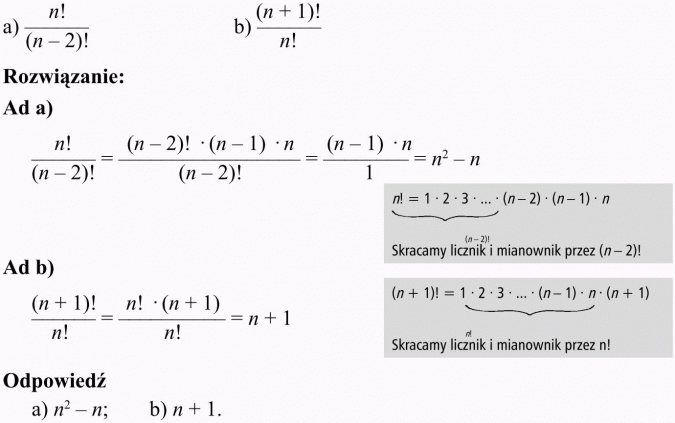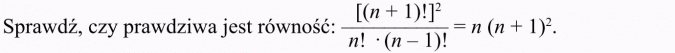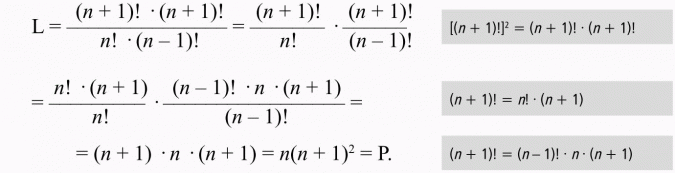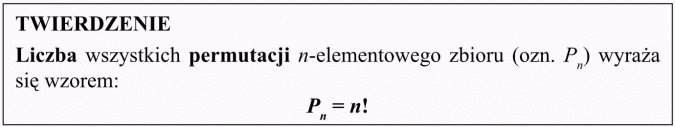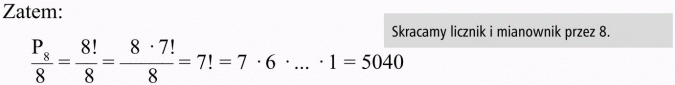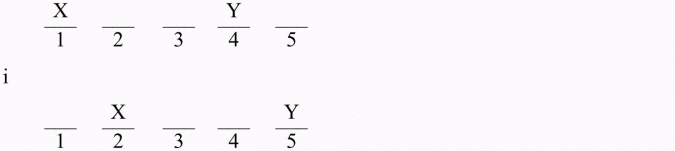Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Zapamiętaj!
Symbolem n! (czytaj: n silnia) oznaczamy iloczyn kolejnych liczb naturalnych od 1 do n włącznie.
Przykłady
Oblicz:
Doprowadź do najprostszej postaci wyrażenia:
Rozwiązanie:
Zajmiemy się przekształceniem lewej strony równości...
Zatem L = P.
Odpowiedź:
Dana równość jest prawdziwa.
Zapamiętaj!
Z permutacjami danego zbioru mamy do czynienia wtedy, gdy porządkujemy elementy danego zbioru (kolejność elementów jest tutaj istotna).
Ankieta złożona ma być z trzech pytań: A, B i C. Na ile sposobów można ją ułożyć zmieniając tylko kolejność pytań?
Ile jest wszystkich liczb czterocyfrowych o różnych cyfrach utworzonych z cyfr 1, 2, 3, 4?
Rozwiązanie:
Wypisywanie wszystkich ustawień cyfr jest dość kłopotliwe. Wyobraźmy sobie, że mamy do uzupełnienia cztery kratki, gdzie każda kratka to jedna z czterech cyfr naszej liczby:
Cyfrą tysięcy może być: 1, 2, 3 lub 4 - mamy cztery możliwości. Po wypełnieniu pierwszej kratki, drugą, czyli cyfrę setek możemy zapisać za pomoca jednej z trzech pozostałych cyfr - mamy trzy możliwości. Cyfrą dziesiątek może być jedna z dwóch pozostałych cyfr, czyli mamy dwie możliwości. Ostatnią kratkę wypełniamy pozostałą, ostatnią cyfrą - mamy jedną możliwość. Zatem wszystkich możliwych ustawień (ciągów) jest:
Odpowiedź
Są 24 takie liczby.
Na ile sposobów może usiąść na ławce 6 osób?
Rozwiązanie:
Odpowiedź
6 osób może usiąść na 720 różnych sposobów.
Ile liczb siedmiocyfrowych można zapisać za pomocą cyfr: 0, 1, 2, 3, 4, 5, 6, jeśli cyfry nie mogą się powtarzać?
Rozwiązanie:
Wszystkich liczb siedmiocyfrowych utworzonych z siedmiu różnych cyfr jest:
Jednak pierwszą cyfrą liczby nie może być zero. Obliczmy, ile jest możliwych takich ustawień, w których 0 jest na pierwszym miejscu:
Odpowiedź
Wszystkich możliwych liczb siedmiocyfrowych, jakie można utworzyć z cyfr: 0, 1, 2, 3, 4, 5, 6 jest 4320.
Liczba permutacji n elementów jest 30 razy mniejsza od liczby permutacji n + 2 elementów. Oblicz n.
Na ile różnych sposobów może usiąść 8 osób przy okrągłym stole, jeżeli:
a) uwzględniamy miejsca zajmowane przy stole (krzesła są ponumerowane),
b) uwzględniamy tylko rozmieszczenie osób względem siebie.
Rozwiązanie:
Ad a)
Sposobów jest tyle, ile permutacji 8-elementowego zbioru, czyli:
Ad b)
Jeżeli uwzględniamy tylko rozmieszczenie osób względem siebie, to znaczy, że za różne sposoby rozmieszczenia osób przy stole uważamy takie dwa, w których przynajmniej jedna z osób ma innego sąsiada po prawej lub lewej stronie. Zatem rozmieszczenie osób nie ulegnie zmianie, jeżeli np. każdą z osób przesadzimy o jedno krzesło (lub więcej, ale wszystkich o tyle samo) w tym samym kierunku (np. zgodnie z ruchem wskazówek zegara). Liczba różnych sposobów rozmieszczenia osób jest więc 8 razy mniejsza niż w sytuacji, gdy krzesła były ponumerowane.
Inaczej: jesli ustalimy miejsce pierwszej osoby (nie ma znaczenia, które krzesło zajmie), to wystarczy rozważyć, jak względem niej można rozmieścić siedem pozostałych osób. Można to uczynić na 7! sposobów (tyle, ile jest permutacji 7-elementowego zbioru), czyli 5040.
Odpowiedź
Jest 5 040 możliwości.
Należy ustawić pięć osób w szeregu tak, aby:
a) osoby X i Y stały obok siebie,
b) pomiędzy osobami X i Y stały dwie osoby.
Na ile sposobów można to zrobić w każdym z wymienionych przypadków?
Rozwiązanie:
Ad a)
Wyobraźmy sobie ten szereg (dla ułatwienia ponumerujmy miejsca w szeregu):
Zastanówmy się, na ile sposobów możemy ustawić osobę X tak, aby osoba Y mogła stać obok niej. Są 4 możliwości: miejsca od 1 do 4 włącznie (X nie może stanąć tylko na końcu, czyli w pozycji 5, ponieważ wtedy dla Y zabraknie miejsca).
X i Y mogą być ustawione w innym uporządkowaniu (X może stać po lewej lub prawej ręce Y). Takich możliwości jest tyle, ile permutacji 2-elementowego zbioru, czyli P2 = 2!
Mamy jeszcze do rozważenia ustawienie pozostałych trzech osób. Mogą one dowolnie zmieniać się miejscami (w każdym przypadku mają do wykorzystania trzy miejsca). Sposobów ustawienia ich w szeregu jest tyle, ile permutacji 3-elementowego zbioru, czyli P3 = 3!
Zatem wszystkich sposobów ustawienia w szeregu 5-osobywm osób X i Y obok siebie jest:
4 · 2! · 3! = 4 · 2 · 6 = 48
Odpowiedź
Wszystkich możliwych ustawień takich, że osoby X i Y stoją obok siebie, jest 48.
Ad b)
Rozważmy ustawienie:
Zatem osobę X można ustawić na 2 sposoby tak, aby osoba Y mogła stać za X o dwie osoby dalej.
X i Y mogą być ustawione w innym uporządkowaniu (X może stać po lewej lub prawej ręce Y). Takich możliwości jest tyle, ile permutacji 2-elementowego zbioru, czyli P2 = 2!
Ustawienie pozostałych trzech osób (analogicznie jak w poprzednim przypadku) może odbyć się na 3! sposobów (P3 = 3!).
Zatem wszystkich sposobów ustawienia w szeregu 5-osobowym tak, aby między osobami X i Y stały 2 osoby, jest:
2 · 2! · 3! = 2 · 2 · 6 = 24
Odpowiedź
Wszystkich możliwych ustawień takich, że pomiędzy osobami X i Y stoją dwie osoby, jest 24.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.