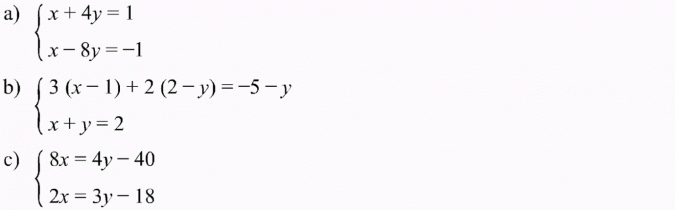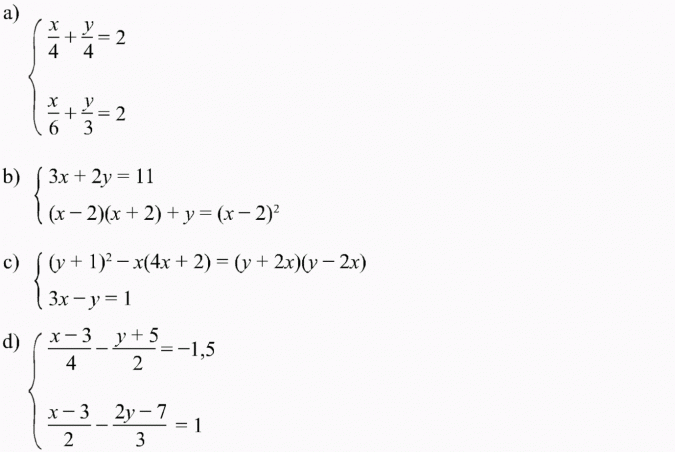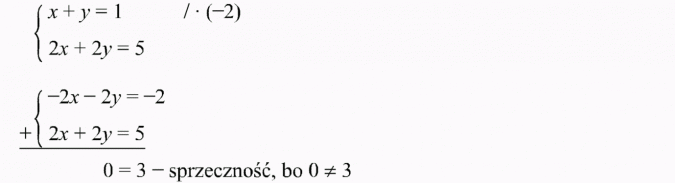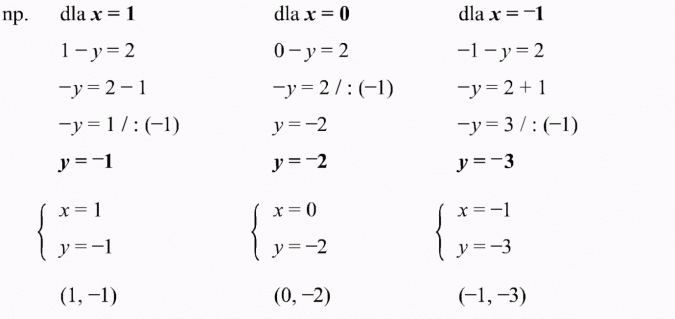Rozwiązywanie układów równań

Metoda przeciwnych współczynników

Przykład 1

Sprawdzenie:

Metoda przeciwnych współczynników. Podstawiam do obu równań w miejsce x liczbę 10, a w miejsce y liczbę 1. Obie równości są prawdziwe, a zatem para liczb (10, 1) jest rozwiązaniem układu.

Jak postępujemy przy rozwiązywaniu układów równań metodą przeciwnych współczynników:

1) Równania przekształcamy tak, aby współczynniki przy tej samej niewiadomej były liczbami przeciwnymi.

2) Dodajemy lewe i prawe strony równań układu (otrzymujemy równanie z jedną niewiadomą).

3) Rozwiązujemy równanie z jedną niewiadomą.

4) Tworzymy ponownie układ równań, dopisując jako drugie równanie, dowolnie wybrane równanie układu.

5) Teraz, stosując metodę podstawiania, rozwiązujemy równanie.

6) Podajemy rozwiązanie układu.

Przykład 2

Rozwiąż układ równań metodą przeciwnych współczynników:

Metoda przeciwnych współczynników. Przy niewiadomej x są liczby przeciwne, dodajemy równania stronami. Lewe strony, prawe strony. Tworzymy ponownie układ równań, dopisując jako drugie równanie, dowolnie wybrane równanie układu. Teraz do II równania w miejsce y podstawiam liczbę 1. Rozwiązuję II równanie. Rozwiązaniem układu jest para lizcb (2, 1).

Sprawdzenie:

Metoda przeciwnych współczynników. Do obu równań w miejsce x podstawiam liczbę 2, a w miejsce y liczbę 1. Sprawdzam, czy zachodzą równości. Obie równości są prawdziwe, zatem para liczb x = 2 i y = 1 jest rozwiązaniem tego układu.

Przykład 3

Rozwiąż układ równań:

Metoda przeciwnych współczynników. W praktyce rzadko zdarza się, aby współczynniki przy tej samej niewiadomej były liczbami przeciwnymi. Do takiej sytuacji można dosyć łatwo doprowadzić. W tym celu obie strony I równania mnożymy przez 2. Przy niewiadomej y są liczby przeciwne, możemy dodawać stronami. Rozwiązuję otrzymane równanie. Do równania x = 3 dopisuję drugie dowolnie wybrane równanie układu, np. x + 2y = 7. Do II równania w miejsce x podstawiam liczbę 3 i rozwiązuję otrzymane równanie. Para liczb (3, 2) jest rozwiązaniem tego układu.

Sprawdzenie:

Metoda przeciwnych współczynników. Do obu równań podstawiam w miejsce x liczbę 3, a w miejsce y liczbę 2. Sprawdzam, czy zachodzą równości. Otrzymałam równości prawdziwe, a zatem para liczb x = i y = 2 jest rozwiązaniem układu.

Przykład 4

Rozwiąż układ równań metodą przeciwnych współczynników

Metoda przeciwnych współczynników. Obie strony I równania mnożę przez 2. Przy niewiadomej y otrzymam liczby przeciwne. Drugie równanie przepisuję bez zmian. Oba równania dodaję stronami (w ten sposób eliminuję niewiadomą y). Rozwiązuję otrzymane równanie. Skracam ułamek, dzieląc licznik i mianownik przez 7. Tworzę nowy układ równań, którego jedynym równaniem jest obliczona wartość x, a drugim dowolne równanie układu. Do II równania za x podstawiam liczbę 2/3 i rozwiązuję otrzymane równanie. (-) : (-) = (+) Para liczb (2/3, 1 1/2) jest rozwiązaniem układu.

Sprawdzenie:

Metoda przeciwnych współczynników. W miejsce x wstawiam liczbę 2/3, a w miejsce y liczbę 3/2. Sprawdzam, czy zachodzą równości. Otrzymaliśmy równości prawdziwe, a więc para liczb (2/3, 1 1/2) jest rozwiązaniem tego układu.

Zadanie 2

Rozwiąż układy równań metodą przeciwnych współczynników:

Rozwiązanie

Metoda przeciwnych współczynników. Obie strony drugiego równania mnożę przez (-1). Przy niewiadomej x otrzymam liczby przeciwne. Równania dodaję stronami. Tworzę nowy układ równań, dopisując do równania x = 1/6 dowolne równanie układu. Do II równania za y podstawiam liczbę 1/6. Rozwiązuję równanie. Rozwiązaniem układu równań jest para liczb. Pierwsze równanie układu doprowadzamy do prostszej postaci. Drugie przepisujemy bez zmian. Niewiadome przenosimy na lewą stronę, a wiadome na prawą (uważaj na znaki przy przenoszeniu). Dodajemy równania stronami (przy niewiadomej y są liczby przeciwne: -1 i 1). Tworzymy nowy układ równań, dopisując drugie równanie. Do II równania za x podstawiam liczbę (-1). para liczb (-1, 3) jest rozwiązaniem tego układu. Zauważ, że jeżeli obie strony I równania podzielę przez (-4), to przy niewiadomej x otrzymam liczby przeciwne. Dodaję równania stronami. Rozwiązuję równanie. Do równania y = 4 dopisuję drugie, dowolnie wybrane równanie układu, np. 2x = 3y - 18. Za y do II równania podstawiam liczbę 4. Para liczb (-3, 4) spełnia ten układ równań.

Zadanie 3

Rozwiąż układy równań dowolną metodą:

Rozwiązanie

Metoda przeciwnych współczynników. W celu pozbycia się ułamków obie strony każdego z równań mnożę przez wspólny mianownik. Wybieram metodę przeciwnych współczynników. Rozwiązaniem układu jest para liczb (4, 4). Drugie równanie doprowadzam do prostszej postaci. Stosuję wzory skróconego mnożenia. Niewiadome przenoszę na lewą stronę równania, a liczby na prawą (uważaj na znaki przy przenoszeniu). Myślę, że metoda przeciwnych współczynników będzie łatwiejsza. Dopisuję drugie równanie (dowolnie wybrane z układu).

Odp.:

Para liczb (1, 4) jest rozwiązaniem tego układu.

Metoda przeciwnych współczynników. I równanie doprowadzam do prostszej postaci, stosując wzory. Wygodnie jest rozwiązać ten układ metodą przeciwnych współczynników. Rozwiązaniem układu jest para liczb (1/4, -1/4). Oba równania doprowadzamy do prostszej postaci, w tym celu obie strony I równania mnożymy przez wspólny mianownik, czyli 4, a drugiego przez 6. Niewiadome przenosimy na lewą stronę, a liczby na prawą (przy przenoszeniu zmieniamy znak na przeciwny). Znowu metoda przeciwnych współczynników wydaje mi się mniej pracochłonna.

Odp.:

Układ równań spełnia para liczb (-13, -10).

Układ równań, którego rozwiązaniem jest jedna para liczb, nazywamy układem oznaczonym lub układem równań niezależnych.

Każdy z rozwiązywanych dotąd układów miał jedno rozwiązanie. Nie zawsze tak jest.

Przykład 1

Metoda przeciwnych współczynników. Sprzeczność, bo 0 != 3.

Takiego układu równań nie spełnia żadna para liczb. Jest to układ sprzeczny, nie ma rozwiązania.

Przykład 2

Metoda przeciwnych współczynników. Otrzymaliśmy dwa jednakowe równania. Rozwiążmy ten układ metodą przeciwnych współczynników. Tożsamość.

Rozwiązaniem takiego układu równań jest nieskończenie wiele par liczb.

Układ równań, ktory posiada nieskończenie wiele rozwiązań, nazywamy układem nieoznaczonym lub układem równań zależnych.

Znajdźmy kilka par liczb, które spełniają ten układ równań. W tym celu zajmijmy się tylko jednym równaniem: x - y = 2, ponieważ drugie równanie jest tożsamościowe. W miejsce x podstawmy dowolną liczbę i obliczamy wartość y:

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Rozwiązywanie układów równań

Metoda przeciwnych współczynników

Zadanie 2

Zadanie 3

Zobacz podobne opracowania

Ciekawostki (0)

Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.

Szukasz szybszego sposobuna zapamiętywanie?

Popularne

Zbliża sięsprawdzian?

Zobacz także

Polecane na dziś

Szukasz szybszego sposobu
na zapamiętywanie?

Zbliża się
sprawdzian?