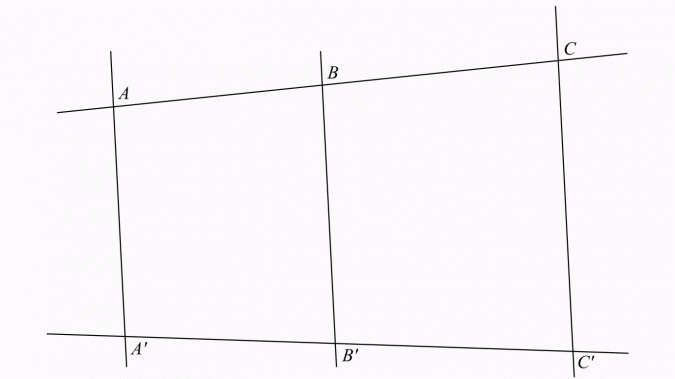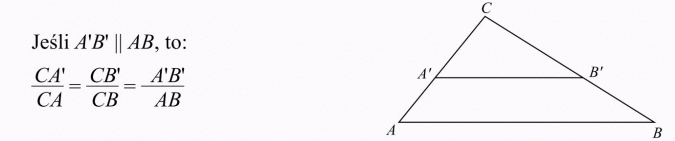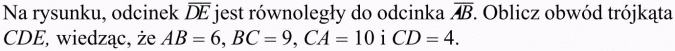Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Jeżeli dwie proste przetniemy prostymi równoległymi, to długości odcinków utworzonych na jednej prostej są proporcjonalne do długości odpowiednich odcinków utworzonych na drugiej prostej.
Inaczej:
Małe twierdzenie Talesa (dotyczące trójkąta)
Jeżeli ramiona kąta przetniemy prostymi równoległymi, to długości odcinków utworzonych na jednym ramieniu kąta są proporcjonalne do długości odpowiednich odcinków utworzonych na drugim ramieniu tego kąta.
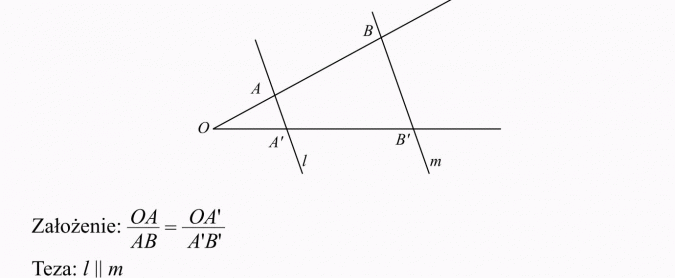
Twierdzenie odwrotne do małego twierdzenia Talesa
Jeżeli długości odcinków wyznaczonych przez dwie proste na jednym ramieniu kąta są proporcjonalne do długości odpowiednich odcinków wyznaczonych na drugim ramieniu kąta, to te proste są równoległe.
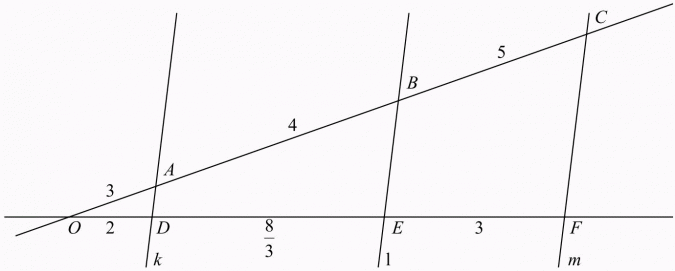
Mając dane, jak na poniższym rysunku, odpowiedz, które spośród prostych k, l, m są równoległe.
Rozwiązanie:
Musimy sprawdzić, czy odpowiednie odcinki są proporcjonalne.
Czy proste k i l są równoległe?
Proste k i l są równoległe.
Czy proste l i m są równoległe?
Proste l i m nie są równoległe.
Czy proste k i m są równoległe?
Odpowiedź
Proste k, l są równoległe.
Prosta m nie jest równoległa do żadnej z prostych k, l.
Rozwiązanie:
Najpierw rysujemy trójkąt i zaznaczamy znane wielkości. Następnie korzystamy z małego twierdzenia Talesa, dotyczącego trójkąta i z twierdzenia Talesa.
Obwód trójkąta CDE znajdujemy, dodając długości jego boków.
Odpowiedź
Obwód trójkąta CDE równa się 10.
Na jednym ramieniu kąta, poczynając od jego wierzchołka, odłożono kolejno odcinki o długościach a, b, c. W rzucie równoległym tych odcinków na drugie ramię kąta otrzymano odcinki kolejno o długościach c, a, b. Wykaż, że liczby a, b, c są równe.
Rozwiązanie:
Nie przerażaj się, widząc słowo „wykaż".
Najpierw wykonujemy rysunek.
To, że w zadaniu jest mowa o rzucie równoległym, oznacza, że na rysunku odcinki łączące ramiona kąta są równoległe.
Piszemy proporcje:
Podstawy trapezu mają długości a = 18 i b = 12, zaś jego ramiona długości c = 15, d = 12. Oblicz długość x, y przedużeń obu ramion trapezu do ich punktu przecięcia.
Rozwiązanie:
Najpierw sporządzamy rysunek.
Wykaż, że odcinek łączący środki przekątnych trapezu jest równoległy do podstaw trapezu.
Rozwiązanie:
Najpierw rysunek:
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.