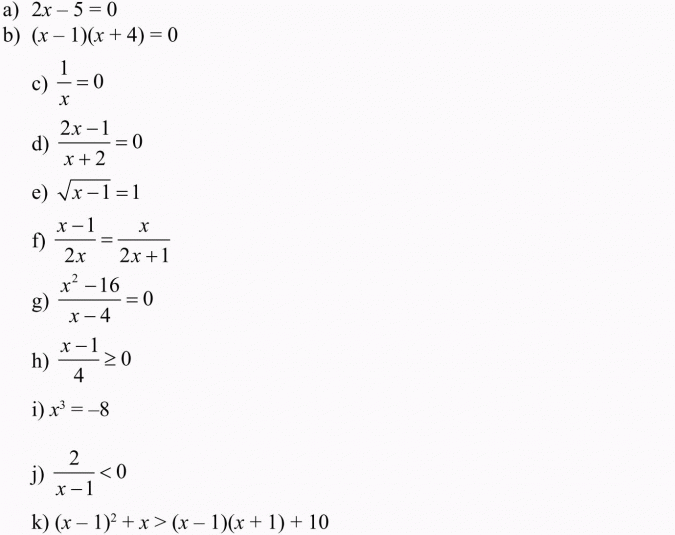Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Przykład
Nazwij podane zdania i oceń ich wartość logiczną.
a) Warszawa jest stolicą Polski lub Kraków jest stolicą Polski.
b) Przekątne rombu przecinają się pod kątem ostrym i dzielą się na pół.
c) Jeżeli liczba naturalna 12 jest podzielna przez 6, to jest podzielna przez 5.
d) Równoległobok jest rombem wtedy i tylko wtedy, gdy ma wszystkie boki równe.
Rozwiązanie:
Ad a)
Z uwagi na występujący w zdaniu spójnik logiczny „lub” zdanie jest alternatywą. Pierwszy człon alternatywy jest zdaniem prawdziwym, natomiast drugi jest zdaniem fałszywym. Całe zdanie jest zatem prawdziwe.
Ad b)
W zdaniu występuje spójnik logiczny „i”, zatem jest to koniunkcja. Pierwszy człon koniunkcji jest fałszywy, drugi natomiast jest prawdziwy. Koniunkcja jest fałszywa.
Ad c)
Zdanie jest implikacją z uwagi na zwrot „jeżeli, to”. Jest to implikacja fałszywa, ponieważ fałszywy jest jej następnik, czyli zdanie po słowie „to”.
Ad d)
Jest to równoważność, ponieważ występuje zwrot „wtedy i tylko wtedy”. Oba zdania składowe są prawdziwe, zatem cała równoważność jest prawdziwa.
Rozwiązanie:
Wyznacz zbiór elementów spełniających formę zdaniową:
Rozwiązanie:
W każdym z przykładów należy wyznaczyć dziedzinę podanej formy zdaniowej, następnie znaleźć rozwiązanie równania lub nierówności i sprawdzić, czy należy do dziedziny.
Pogłębiaj wiedzę w temacie: Zdania logiczne. Prawa De Morgana
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
