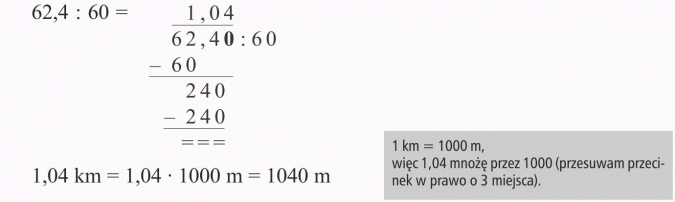Dzielenie ułamków (na poziomie ucznia klasy 5)

Na początku wyjaśnię Ci przypadki dzielenia pozornie nie mające nic wspólnego z tytułem rozdziału. Mam na myśli dzielenie dwóch liczb naturalnych,w wyniku którego otrzymujesz ułamek dziesiętny.

Dzielenie ułamków. Obliczam 84 : 5. W tym miejscu liczba kończy się, ale dzielenie nie zostało zakończone. Rozszerzam dzielną 84 = 84,0; spisuję 0 i liczę dalej.

PAMIĘTAJ

Przecinek ilorazu znajduje się nad przecinkiem dzielnej.

Dzielenie ułamków. Dzielna, dzielnik, iloraz.

Przykłady

Dzielenie ułamków. Ponieważ dzielenie nie skończyło się po rozszerzeniu 403 = 403,0, dopisuję następne 0. Liczbę 91 rozszerzyłam do trzeciego miejsca po przecinku. Każde dzielenie możesz sprawdzić, mnożąc iloraz przez dzielnik.

UWAGA!

Jeśli pomimo kolejnych rozszerzeń dzielenie nie kończy się, a cyfry w ilorazie zaczynają się powtarzać, to masz do czynienia z tzw. ułamkiem okresowym, o którym dowiesz się w następnych klasach.

Zadanie 1

Za 8 foteli zapłacono 1166 zł. Ile kosztował 1 fotel?

Rozwiązanie:

Dzielenie ułamków. Dzielę kwotę, którą zapłacono, przez ilość foteli. Zera po przecinku nic nie znaczą - opuszczam je.

Odpowiedź:

Jeden fotel kosztował 145,75 zł.

Teraz zajmę się przykładami dzielenia ułamków dziesiętnych przez liczby naturalne. Dzielenie takie może zakończyć się na ostatniej cyfrze dzielnej, jak w przypadku działania 31,38 : 6

lub musisz rozszerzać dzielną, jak w przypadku działania 148,7 : 2

Dzielenie ułamków. Po spisaniu 7, dzielenie nie kończy się, więc dopisuję 0 w dzielnej.

Przykłady

Dzielenie ułamków. Pamiętaj o przecinku w ilorazie!

Zadanie 2

Samochód jedzie z prędkością 62,4 km/h. Ile metrów przejedzie ten samochód w ciągu minuty?

Rozwiązanie:

Jak już wcześniej wyjaśniłam, prędkość 64,4 km/h oznacza, że w ciągu godziny ten samochód przejedzie 62,4 km.

Ponieważ 1 godz. = 60 min, więc w ciągu 1 minuty przejedzie 60 razy krótszą drogę.

Dzielenie ułamków. 1 km = 1000 m, więc 1,04 mnożę przez 1000 (przesuwam przecinek w prawo o 3 miejsca).

Odpowiedź:

W ciągu minuty samochód przejedzie 1040 m.

WAŻNE!

Dzieląc liczbę przez ułamek dziesiętny, musisz w dzieleniu i dzielnej przesunąć przecinek o tyle miejsc w prawo, aby dzielnik stał się liczbą naturalną.

Przesunięcie przecinka w dzielnej i dzielniku o tyle samo miejsc jest równoznaczne z pomnożeniem obu liczb przez 10 lub 100, lub 1000, co, jak wiesz, nie zmienia wyniku.

Przykłady

Dzielenie ułamków. 1 miejsce po przecinku, po przesunięciu przecinka o 1 miejsce w prawo. Teraz dzielę jak w poprzednich przykładach. Zwróć uwagę na fakt, że sprawdzam poprawność działania 27,96 : 1,2, zatem mnożę iloraz (23,3) przez dzielnik, czyli 1,2. 28,8 = 28,800 i teraz przesuwam przecinek.

Zadanie 3

Jedna pomadka waży 0,02 kg. Ile pomadek jest w 1,5 kg?

Rozwiązanie:

Ilość sztuk obliczam, dzieląc 1,5 kg przez masę jednej czekoladki, czyli 0,02 kg.

Dzielenie ułamków. W dzielnej i dzielniku przesunęłam przecinek o 2 miejsca. Mnożę 75 x 2 = 150 i od prawej strony odliczam 2 miejsca po przecinku.

Odpowiedź:

W 1,5 kg jest 75 czekoladek.

Zadanie 4

Cena 1 kg papryki wynosiła 7,50 zł/kg. Ile dag papryki kupiła Agnieszka, jeżeli zapłaciła 2,10 zł?

Rozwiązanie:

Korzystam z grafu (patrz poprzedni rozdział, s. 68):

Dzielenie ułamków. Masa kupionego produktu, cena, kwota do zapłaty. Skróciłam, przesunęłam przecinek w dzielnej i dzielniku o 1 miejsce. 1 kg = 100 dag.

Odpowiedź:

Agnieszka kupiła 28 dag papryki.

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Dzielenie ułamków (na poziomie ucznia klasy 5)