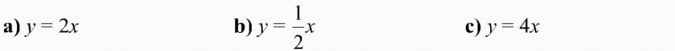Funkcja liniowa i jej własności

Funkcję określoną wzorem y = ax + b, gdzie a i b są dowolnymi liczbami rzeczywistymi nazywamy funkcją liniową.

Liczbę a nazywamy współczynnikiem kierunkowym prostej, liczbę b wyrazem wolnym.

Dziedziną funkcji liniowej jest zbiór liczb rzeczywistych.

Wykresem funkcji liniowej jest prosta.

Aby narysować tę prostą, wystarczy znaleźć dwa dowolne jej punkty.

Przykład

Narysuj wykres funkcji y = 2x - 1.

Wiemy, że wykresem funkcji liniowej jest prosta. Zatem dla sporządzenia wykresu wystarczy znaleźć dwa punkty należące do tej prostej.

W tym celu do wzoru funkcji y = 2x - 1 podstawiamy za x np. liczby 0 oraz 1 (argumenty x dobieramy tak, aby obliczenia były jak najprostsze).

Funkcja liniowa i jej własności. Otrzymane punkty (0, -1) oraz (1, 1) zaznaczamy w układzie współrzędnych, następnie rysujemy prostą przechodzącą przez te punkty. Otrzymaliśmy wykres funkcji y = 2x-1. Otrzymaną prostą podpisujemy wzorem funkcji.

Zadanie 1

W jednym układzie współrzędnych narysuj wykresy funkcji:

Rozwiązanie:

Funkcja liniowa i jej własności. Obliczam wartość funkcji. Do wzoru funkcji y = 2x podstawiam za x liczbę 0 oraz 1. Otrzymane punkty zaznaczam w układzie współrzędnych i rysuję wykres funkcji. Obliczam wartość funkcji. Otrzymane punkty zaznaczam w układzie współrzędnych i rysuję wykres funkcji. Zauważ, że: Dla funkcji liniowej y = ax + b, jeżeli b = 0, to funkcja przyjmuje postać y = ax. Jej wykres przechodzi zawsze przez początek układu współrzędnych (punkt (0, 0)) oraz przez punkt o współrzędnych (1, a). Jeżeli: a większe od 0, to wykres funkcji y = ax przechodzi przez I i III ćwiartkę; a mniejsze od 0, to wykres funkcji y = ax przechodzi przez II i IV ćwiartkę układu współrzędnych.

Zadanie 2

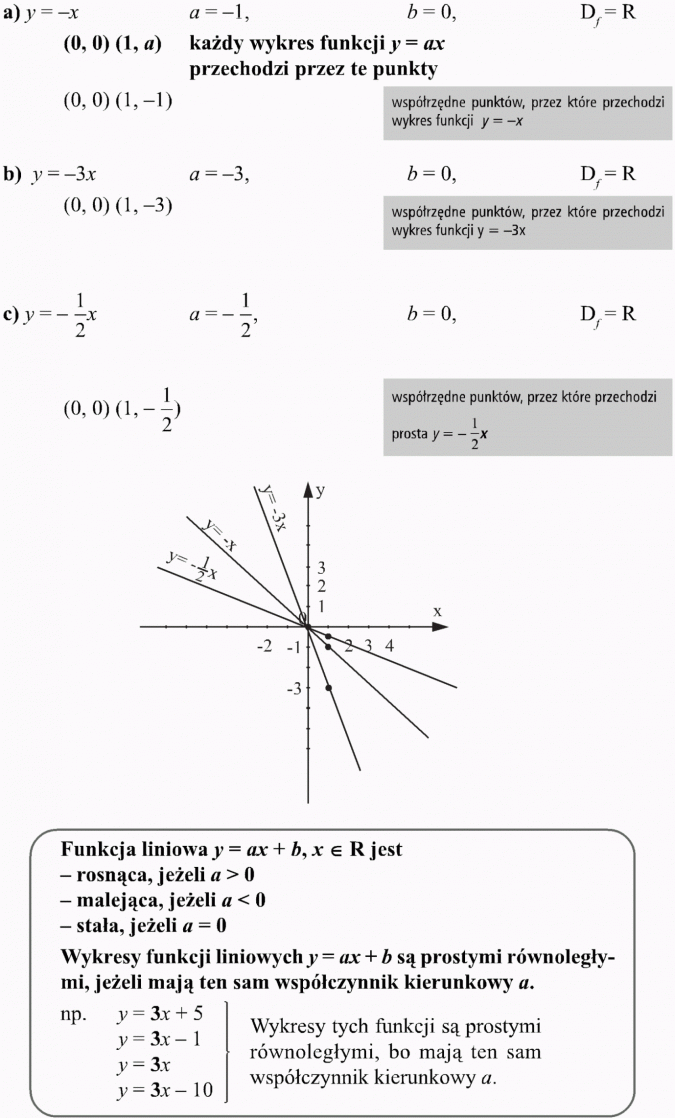
Narysuj w jednym układzie współrzędnych wykresy funkcji:

Rozwiązanie:

Funkcja liniowa i jej własności. Każdy wykres funckji y = ax przechodzi przez te punkty. Współrzędne punktów, przez które przechodzi wykres funkcji y = -x. Współrzędne punktów, przez które przechodzi wykres funkcji y = -3x. Współrzędne punktów, przez które przechodzi prosta y = -1/2x. Funkcja liniowa y = ax + b, x należy do R jest rosnąca, jeżeli a większe od 0; malejąca, jeżeli a mniejsze od 0; stała, jeżeli a = 0. Wykresy funkcji liniowych y = ax + b są prostymi równoległymi, jeżeli mają ten sam współczynnik kierunkowy a. Wykresy tych funkcji są prostymi równoległymi, bo mają ten sam współczynnik kierunkowy a.

Zadanie 3

Napisz wzór funkcji, której wykresem jest prosta przechodząca przez początek układu współrzędnych i punkt:

Rozwiązanie:

Funkcja liniowa i jej własności. Ogólna postać funkcji liniowej, której wykres przechodzi przez początek układu współrzędnych. Do wzoru y = ax w miejsce x i y podstawiam współrzędne punktu A (x = 1, y = 5). Obliczam współczynnik a. Do wzoru y = ax podstawiam w miejsce a liczbę 5. Szukany wzór funkcji. Postępuję podobnie jak w punkcie a). Do wzoru funkcji y = ax, w miejsce x i y podstawiam współrzędne punktu B. Szukany wzór funkcji.

Zadanie 4

Napisz wzór funkcji liniowej, której wykres przechodzi przez początek układu współrzędnych i jest równoległy do wykresu funkcji:

Rozwiązanie:

Funkcja liniowa i jej własności. Ogólna postać wzoru szukanej funkcji, należy znaleźć współczynnik a. Bo szukana prosta ma być równoległa do wykresu funkcji y = 4x - 5 (wykresy równoległe mają ten sam współczynnik kierunkowy a). Wzór szukanej funkcji. Równanie prostej przechodzącej przez początek układu współrzędnych. Bo szukana prosta ma być równoległa do prostej y = -5x + 6 (a = -5). Wzór szukanej funkcji.

Zadanie 5

Dana jest funkcja y = 2x - 3

a) oblicz wartość funkcji dla argumentu x = 4

b) znajdź argument, dla którego wartość funkcji wynosi -5

c) oblicz miejsce zerowe funkcji

d) narysuj wykres funkcji

e) podaj współrzędne punktów, w których wykres funkcji przecina osie układu współrzędnych

f) sprawdź, czy punkty A = (-2, -7), B = (2, 3) należą do wykresu funkcji

g) czy funkcja jest rosnąca, malejąca czy stała?

Funkcja liniowa i jej własności. Pamiętaj! x - argument funkcji, y - wartość funkcji. Do wzoru funkcji podstawiam za x liczbę 4 i obliczam wartość funkcji, czyli y. Dla argumentu 4 wartość funkcji wynosi 5. Do równania za y pdostawiam liczbę (-5) i obliczam argument funkcji. Wartość funkcji wynosi -5 dla argumentu x = -1. Miejsce zerowe funkcji to ten argument x, dla którego wartość funkcji (czyli y) równa jest 0. Obliczam miejsce zerowe funkcji, za y podstawiam liczbę 0. Miejsce zerowe funkcji wynosi 1 1/2. Korzystam ze wzoru na miejsce zerowe funkcji y = ax + b. -b we wzorze oznacza, że mam podstawić liczbę przeciwną do b (liczbą przeciwną do (-3) jest 3). Funkcja ma jedno miejsce zerowe x0 = 1 1/2. Wykresem funkcji y = 2x - 3 jest prosta. Wystarczy znaleźć dwa dowolne punkty, przez które ta prosta przechodzi. Wygodnie jest wybrać punkty charakterystyczne i łatwe do obliczeń. Punkty te to... Warto pamiętać! Miejsce zerowe funkcji. Jeśli a != 0, to wykres funkcji y = ax + b przecina oś x w punkcie (x0, 0), oś y w punkcie (0, b). Wykres funkcji... w tym punkcie przecina oś x. Wykres funkcji... w tym punkcie przecina oś y. I sposób (graficzny). Na podstawie wykresu odczytujemy, który punkt należy do wykresu naszej funkcji. Ten punkt należy do wykresu. Ten punkt nie należy do wykresu funkcji. Sprawdzam, czy dla argumentu x = -2 wartość funkcji y = -7. W tym celu do wzoru funkcji y = 2x - 3 podstawiam za x liczbę -2, za y liczbę -7. Punkt A należy do wykresu funkcji y = 2x - 3. Teraz sprawdzam, czy punkt B należy do wykresu funkcji. Punkt B nie należy do wykresu funkcji. Funkcja jest rosnąca, bo a większe od 0.

Zadanie 6

Dana jest funkcja y = -3x + 2

a) narysuj wykres funkcji

b) oblicz jej miejsca zerowe

c) jaka jest wartość funkcji dla argumentu x = -1

d) dla jakiego argumentu funkcja przyjmuje wartość 5

e) podaj współrzędne punktów przecięcia wykresu funkcji z osiami układu współrzędnych

f) czy funkcja jest malejąca, rosnąca czy stała?

Rozwiązanie:

Funkcja liniowa i jej własności. Współrzędne punktów, przez które przechodzi wykres funkcji y = ax + b. Wzór na miejsce zerowe funkcji y = ax + b. Miejsce zerowe funkcji y. Obliczam wartość funkcji... dla argumentu x = -1 (do wzoru funkcji y = -3x + 2 w miejsce x podstawiam liczbę -1). Dla argumentu x = -1 wartość funkcji wynosi 5. Do wzoru funkcji y... wstawiam liczbę 5 i obliczam argument x. Funkcja y... przyjmuje wartość 5 dla argumentu x = -1. Współrzędne punktu przecięcia wykresu funkcji y = ax + b z osią x. W tym punkcie wykres funkcji y = -3x + 2 przecina oś x. Współrzędne punktu przecięcia wykresu funkcji y = ax + b z osią y. W tym punkcie wykres funkcji y... przecina oś y. Jest to funkcja malejąca, bo a mniejsze od 0.

Zadanie 7

Dana jest funkcja y = x + 3. Dla jakich argumentów funkcja przyjmuje wartości dodatnie, a dla jakich ujemne?

Rozwiązanie: Problem ten można rozwiązać dwoma sposobami:

Funkcja liniowa i jej własności. I sposób (rachunkowy). Funkcja przyjmuje wartości dodatnie (do tej nierówności w miejsce y podstawiam x + 3, bo y = x + 3, następnie rozwiązuję otrzymaną nierówność. Dla argumentów większych od -3 funkcja y = x + 3 przyjmuje wartości dodatnie. Teraz obliczam, dla jakich argumentów funkcja y = x + 3 przyjmuje wartości ujemne. Funkcja przyjmuje wartości ujemne, w miejsce y podstawiam x + 3, bo y = x + 3. Dla argumentów mniejszych od -3 funkcja y = x + 3 przyjmuje wartości ujemne. II sposób (odczytuję z wykresu). Sporządzam wykres funkcji y = x + 3 oraz obliczam miejsce zerowe. Punkty należące do wykresu funkcji y = x + 3. Miejsce zerowe funkcji.

Z wykresu funkcji odczytujemy, że dla argumentów x > -3 funkcja przyjmuje wartości dodatnie (wykres leży nad osią x, współrzędne y tej części wykresu są dodatnie). Zapisujemy:

y > 0 dla x > -3

np. dla x = 2, y = 5 > 0

Dla tych argumentów, dla których wykres leży pod osią X, funkcja przyjmuje wartości ujemne (współrzędne y punktów wykresu są ujemne).

Zapisujemy:

y < 0 dla x < -3

np. dla x = -7, y = -4 < 0

Odp.: Funkcja przyjmuje wartości dodatnie (y > 0) dla x > -3, natomiast wartości ujemne (y < 0) dla x < -3.

Zadanie 8

Funkcja liniowa i jej własności. Dana jest funkcja.

a) sporządź wykres funkcji

b) oblicz jej miejsce zerowe

c) dla jakich argumentów funkcja przyjmuje wartości dodatnie, a dla jakich ujemne

d) dla jakich argumentów funkcja przyjmuje wartości większe od 2

Rozwiązanie:

Funkcja liniowa i jej własności. Punkty należące do wykresu. Miejsce zerowe funkcji. Wzór na miejsce zerowe funkcji y = ax + b. Miejsce zerowe funkcji wynosi -10. Funkcja przyjmuje wartości dodatnie. Dla argumentów większych od -10 funkcja przyjmuje wartości dodatnie. Dla argumentów mniejszych od -10 funkcja przyjmuje wartości ujemne. Funkcja przyjmuje wartości większe od 2 (w miejsce y podstawiamy...). Dla argumentów większych od -6 funkcja przyjmuje wartości większe od 2. Sprawdźmy!

Zadanie 9

Dana jest funkcja y = -x + 3:

a) sporządź wykres tej funkcji

b) oblicz jej miejsce zerowe

c) dla jakich argumentów funkcja przyjmuje wartości dodatnie, a dla jakich ujemne.

Rozwiązanie:

Funkcja liniowa i jej własności. Punkty należące do wykresu funkcji y = -x + 3. Miejsce zerowe funkcji. Funkcja przyjmuje wartości dodatnie. Przy mnożeniu obu stron nierówności przez liczbę ujemną, pamiętaj, żeby zmienić znak nierówności.

Funkcja przyjmuje wartości dodatnie dla argumentów mniejszych od 3.

Funkcja liniowa i jej własności. Funkcja przyjmuje wartości ujemne.

Dla argumentów większych od 3 funkcja przyjmuje wartości ujemne.

Zadanie 10

Wykres funkcji liniowej przechodzi przez punkt A = (1, 3) i jest równoległy do wykresu funkcji y = 2x - 1:

a) napisz wzór tej funkcji

b) sporządź wykresy obu funkcji.

Funkcja liniowa i jej własności. Postać szukanej funkcji; należy znaleźć współczynniki a i b. Ponieważ wykres szukanej funkcji jest równoległy do wykresu funkcji y = 2x - 1. Przypomnienie: wykresy dwóch funkcji liniowych są równoległe, gdy mają te same współczynniki liczbowe a (b jest dowolne). Szukana funkcja ma postać... Wykres szukanej funkcji przechodzi przez punkt A = (1, 3), to znaczy, że współrzędne tego punktu muszą spełniać równanie funkcji (współrzędne punktu A podstawiam do równania...). Wzór szukanej funkcji. Punkty należące do wykresu funkcji y...

Zadanie 11

Funkcja liniowa i jej własności. Napisz wzór funkcji, której wykres jest równoległy do wykresu funkcji y = -3x + 1/2 i przecina oś y w punkcie (0, -5).

Rozwiązanie:

Funkcja liniowa i jej własności. Postać szukanej funkcji. Bo wykres szukanej funkcji jest równoległy do wykresu funkcji... (proste równoległe mają ten sam współczynnik kierunkowy a). Bo wykres funkcji przecina oś y w punkcie (0, b), czyli (0, -5).

Odp.: Szukana funkcja wyraża się wzorem y = -3x - 5.

Zadanie 12

Funkcja liniowa i jej własności. Współczynnik kierunkowy pewnej prostej wynosi -1/3. Wykres tej funkcji przecina oś y w punkcie (0, 3). Napisz równanie opisujące tę funkcję. Sporządź jej wykres.

Rozwiązanie:

Funkcja liniowa i jej własności. Postać szukanej funkcji. a - współczynnik kierunkowy prostej. Bo wykres funkcji przecina oś y w punkcie (0, b), czyli (0, 3). Równanie szukanej funkcji (do równania y... podstawiam a...). Wykres. Punkty, przez które przechodzi wykres funkcji...

Zadanie 13

Znajdź równanie prostej przechodzącej przez punkty

A = (0, 5), B = (1, 2).

Rozwiązanie:

Funkcja liniowa i jej własności. Ogólna postać szukanej funkcji, należy wyznaczyć a i b. Do wzoru y = ax + b podstawiam współrzędne punktu A. II sposób... Do równania y = ax + b podstawiam współrzędne punktu B (x = 1, y = 2), natomiast za b podstawiam liczbę 5 (wcześniej obliczoną). Wzór szukanej funkcji (do równania y = ax + b podstawiam a = -3, b = 5).

Odp.: Szukana prosta ma wzór: y = -3x + 5.

Zadanie 14

Funkcja opisana jest wzorem y = -2x + 4.

a) oblicz miejsce zerowe tej funkcji

b) podaj zbiór tych argumentów, dla których funkcja przyjmuje wartości większe od 8

c) sprawdź rachunkowo, czy punkty A = (2, 3), B = (3, -2) należą do wykresu tej funkcji.

Rozwiązanie:

Funkcja liniowa i jej własności. I sposób (ze wzoru). Miejsce zerowe funkcji y = -2x + 4. II sposób (z definicji). Bo miejsce zerowe funkcji to ten argument x, dla którego wartość funkcji wynosi 0 (y = 0). Miejsce zerowe funkcji wynosi 2. Funkcja przyjmuje wartości większe od 8. Do nierówności y większe od 8, w miejsce y podstawiam -2x + 4 (bo y = -2x + 4). Uwaga na znak nierówności! Dla argumentów mniejszych od -2 funkcja y = -2x + 4 przyjmuje wartości większe od 8. Sprawdzam rachunkowo, czy punkt A = (2, 3) należy do wykresu funkcji. Sprawdzam, czy współrzędne punktu A spełniają równanie funkcji y = -2x + 4 (podstawiam do równania za x liczbę 2, za y liczbę 3). Punkt A = (2, 3) nie należy do wykresu funkcji. Sprawdzam podobnie jak dla punktu A. Punkt B należy do wykresu funkcji y = -2x + 4.

Zadanie 15

Napisz równanie prostej przechodzącej przez punkty

A = (1, 5), B = (-2, -1).

Rozwiązanie:

Funkcja liniowa i jej własności. Ogólna postać równania prostej, szukamy a i b. Do zapisanego równania prostej podstawiam w miejsce x i y najpierw współrzędne punktu A (otrzymuję I równanie), potem współrzędne punktu B (II równanie). Otrzymuję układ 2 równań o niewiadomych a i b. Następnie rozwiązuję układ równań. Rozwiązaniem układu równań jest para liczb (2, 3). Znalezione współczynniki a i b podstawiamy do ogólnego wzoru funkcji y = ax + b.

Odp.: Wzór szukanej funkcji ma postać y = 2x + 3.

Zadanie 16

Dana jest funkcja y = - 2x + 3

a) narysuj wykres tej funkcji

b) znajdź jej miejsce zerowe

c) oblicz wartość tej funkcji dla argumentu 4,5

d) znajdź argument, dla którego wartość funkcji wynosi 4,5

e) wyznacz współrzędne punktów przecięcia się tej prostej z osiami układu współrzędnych

f) sprawdź, czy punkt (1, 2) należy do wykresu tej funkcji.

Rozwiązanie:

Funkcja liniowa i jej własności. I sposób (ze wzoru). II sposób (z definicji). Do wzoru funkcji y = -2x + 3 w miejsce y podstawiam 0. Miejsce zerowe funkcji y = -2x + 3 wynosi 1 1/2. Pamiętaj! x - argument funkcji, y - wartość funkcji. Dla argumentu 4,5 wartość funkcji wynosi -6. Do wzoru funkcji y = -2x + 3 podstawiam w miejsce y liczbę 4,5 i obliczam x. Wartość funkcji wynosi 4,5 dla argumentu -3/4. Wykres funkcji y = ax + b przecina oś x w punkcie (x0, 0), a oś y w punkcie (0, b). Punkt przecięcia wykresu z osią x, punkt przecięcia wykresu z osią y. Współrzędne tych punktów można również odczytać z wykresu funkcji. Aby sprawdzić, czy punkt należy do wykresu funkcji, trzeba jego współrzędne podstawić do wzoru funkcji i sprawdzić, czy spełniają równanie funkcji. Punkt (1, 2) nie należy do wykresu funkcji y = -2x + 3.

Zadanie 17

Punkty A = (1, 8) i B = (-4, -2) należą do wykresu funkcji y = ax + b

a) znajdź wzór tej funkcji

b) oblicz pole figury ograniczonej wykresem tej funkcji oraz osiami układu współrzędnych.

Rozwiązanie:

Funkcja liniowa i jej własności. Do ogólnego wzoru funkcji y = ax + b w miejsce x i y podstawiam współrzędne najpierw punktu A (otrzymuję I równanie), potem punktu B (II równanie). Rozwiązuję otrzymany układ równań, znajdując współczynniki a i b. Układ równań rozwiązuję metodą przeciwnych współczynników. Otrzymane współczynniki a i b podstawiam do równania y = ax + b. Wzór szukanej funkcji. Rysuję wykres funkcji y = 2x + 6. Znajduję współrzędne punktów, w których wykres funkcji przecina osie układu współrzędnych. Punkt przecięcia wykresu z osią x i osią y. Po narysowaniu wykresu funkcji znajduję figurę ograniczoną tym wykresem oraz osiami układu współrzędnych. Tą figurą jest trójkąt prostokątny KOM. Pole trójkąta prostokątnego jest równe połowie iloczynu jego przyprostokątnych.

Odp.: Pole trójkąta wynosi 9.

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Funkcja liniowa i jej własności