Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Mamy dane dwa zbiory: zbiór X i zbiór Y. Jeżeli każdemu elementowi zbioru X przyporządkujemy dokładnie jeden element zbioru Y, to takie przyporządkowanie nazywamy funkcją na zbiorze X o wartościach w zbiorze Y.
Zbiór X nazywamy dziedziną funkcji (Df).
Element x ze zbioru X nazywamy argumentem funkcji.
Zbiór Y nazywamy przeciwdziedziną funkcji.
Element y zbioru Y przyporządkowany elementowi x ze zbioru X nazywamy wartością funkcji dla argumentu x.
Zmienną x nazywamy też zmienną niezależną, a y zmienną zależną.
Bardzo ważne!
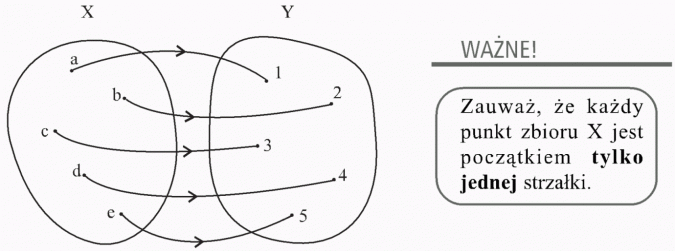
Dla każdego argumentu funkcja przyjmuje dokładnie jedną wartość (z jednego punktu grafu może wychodzić tylko jedna strzałka).
Funkcje oznaczamy małymi literami: f, g, h,...
Nasza funkcja f jest ze zbioru {a, b, c, d, e} do zbioru {1, 2, 3, 4}.
Funkcja f liczbie a przyporządkowuje liczbę 2.
Zapisujemy to tak:
f(a) = 2 - czytamy: f od a równa się 2
Liczbie b funkcja f przyporządkowuje liczbę 1, piszemy:
f(b) = 1 - czytamy: f od b równa się 1
Liczbie c funkcja f przyporządkowuje liczbę 3, piszemy:
f(c) = 3 - czytamy: f od c równa się 3
Liczbie d funkcja f przyporządkowuje liczbę 4, co zapisujemy:
f(d) = 4 - czytamy: f od d równa się 4
lub dla argumentu d wartość funkcji wynosi 4.
Liczbie e funkcja f przyporządkowuje liczbę 5, piszemy:
f(e) = 5 - czytamy: f od e równa się 5
lub: dla argumentu e wartość funkcji wynosi 5.
Uwaga!
Nie każde przyporządkowanie między dwoma zbiorami nazywa się funkcją.
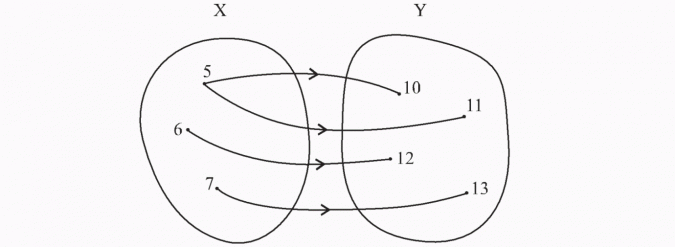
Funkcją nazywamy tylko takie przyporządkowanie, według którego każdemu elementowi z dziedziny (ze zbioru X) przyporządkowany jest dokładnie jeden element z przeciwdziedziny (ze zbioru Y).
Ten graf nie opisuje funkcji, bo liczbie 5 ze zbioru X przyporządkowane zostały dwie liczby: 10 i 11 ze zbioru Y. Zgodnie z definicją funkcji każdemu elementowi zbioru X ma być przyporządkowany dokładnie jeden element zbioru Y.
Przykład 1
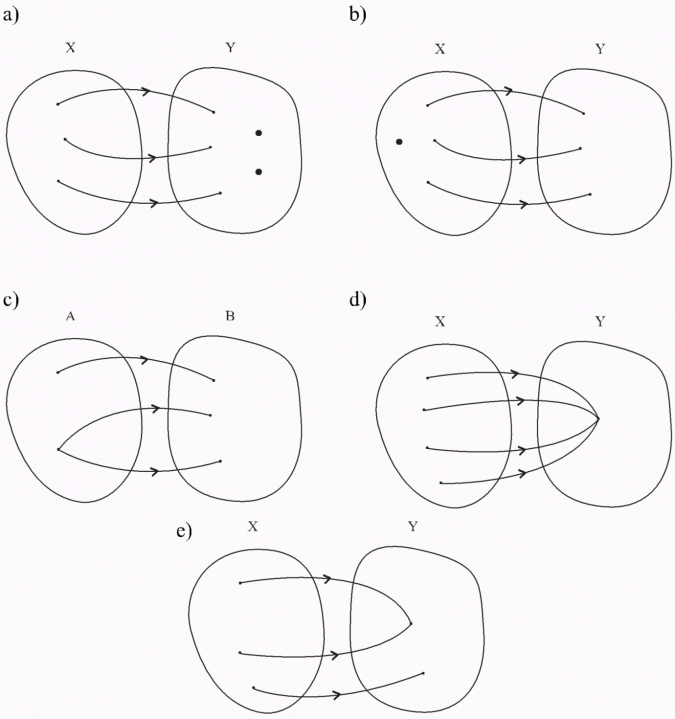
Który z grafów określa funkcję:
Rozwiązanie:
Przy rozwiązywaniu tych przykładów będziemy korzystać z definicji funkcji. Sprawdzamy, czy każdemu elementowi ze zbioru X jest przyporządkowany dokładnie jeden element ze zbioru Y.
a) tak, to przyporządkowanie jest funkcją;
b) ten graf nie opisuje funkcji, gdyż nie każdemu elementowi ze zbioru X jest przyporządkowany element ze zbioru Y. W zbiorze X pozostał jeden element „wolny”;
c) ten graf nie opisuje funkcji, gdyż jednemu elementowi ze zbioru A przypo-rządkowano dwa elementy ze zbioru B;
d) ten graf opisuje funkcję;
e) to przyporządkowanie jest funkcją.
Jeżeli ci trudno określić, czy dane przyporządkowanie jest funkcją, to dobrym przykładem funkcji jest przyporządkowanie ze zbioru listów do zbioru skrzynek (zbiór X - zbiór listów, zbiór Y - zbiór skrzynek). Każdy list musi być wysłany (z def. „każdemu elementowi zbioru X...”).
Jednego listu nie można wrzucić do kilku skrzynek (... jest przyporządkowany dokładnie jeden element zbioru y). Ale wszystkie listy (elementy zbioru X) można wrzucić do jednej skrzynki.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.