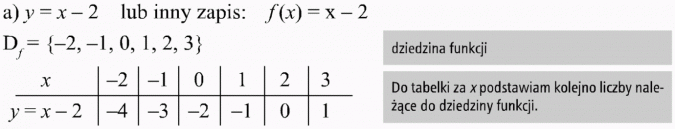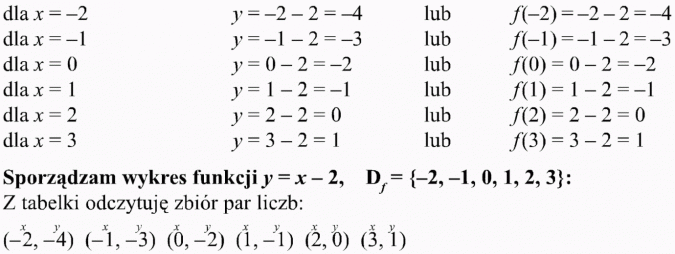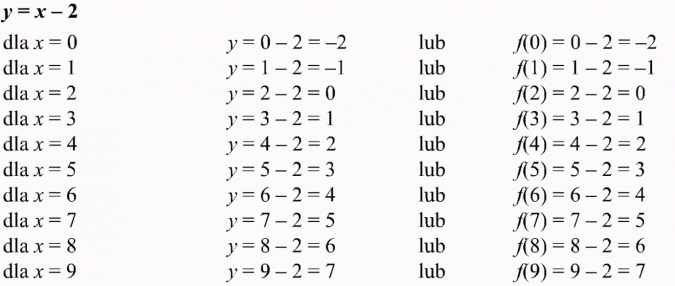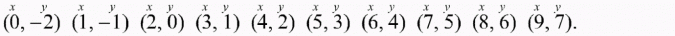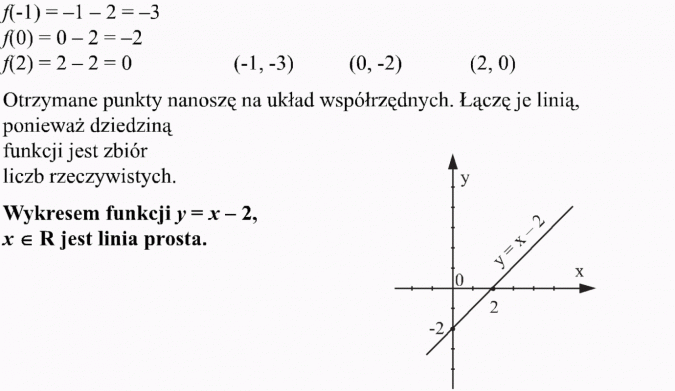Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
1. Opis słowny
2. Graf
3. Tabelka
4. Wzór
5. Wykres
Poniżej jedną funkcję przedstawię na 5 sposobów.
1) Funkcja opisana słownie:
Każdej liczbie naturalnej mniejszej od 8 przyporządkujemy liczbę o 2 większą.
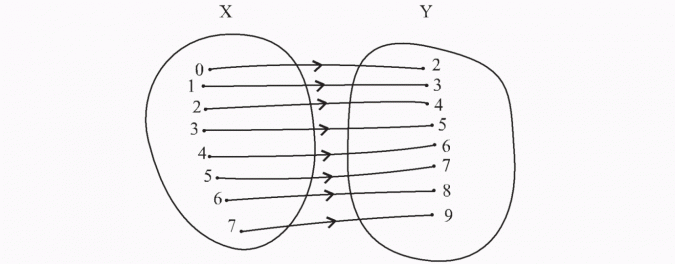
2)Funkcja przedstawiona grafem:
Liczby naturalne to: 0, 1, 2, 3, 4, ...
3) Funkcja przedstawiona za pomocą tabelki:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
W tabelce w I wierszu umieszczamy argumenty (x), w II wierszu wartości funkcji przyporządkowane danym argumentom (y).
4) Funkcja opisana wzorem:
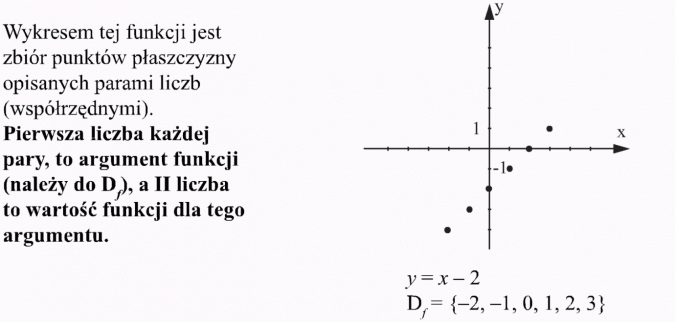
5) Funkcja przedstawiona za pomocą wykresu:
Wykresem funkcji jest zbiór punktów płaszczyzny, których pierwsza współrzędna (x) jest argumentem funkcji, a druga współrzędna (y) jest wartością funkcji dla tego argumentu.
Odczytuję z tabelki współrzędne punktów:
Funkcja ta:
- argumentowi x = 0 przyporządkowuje wartość y = 2, co zapisujemy:
f(0) = 2 (czytamy: f od zera równa się 2);
- argumentowi x = 1 przyporządkowuje wartość y = 3, co zapisujemy:
f(1) = 3 (czytamy: f od 1 równa się 3);
- argumentowi x = 2 przyporządkowuje wartość y = 4, co zapisujemy:
f(2) = 4 (czytamy: f od dwóch równa się 4);
itd.
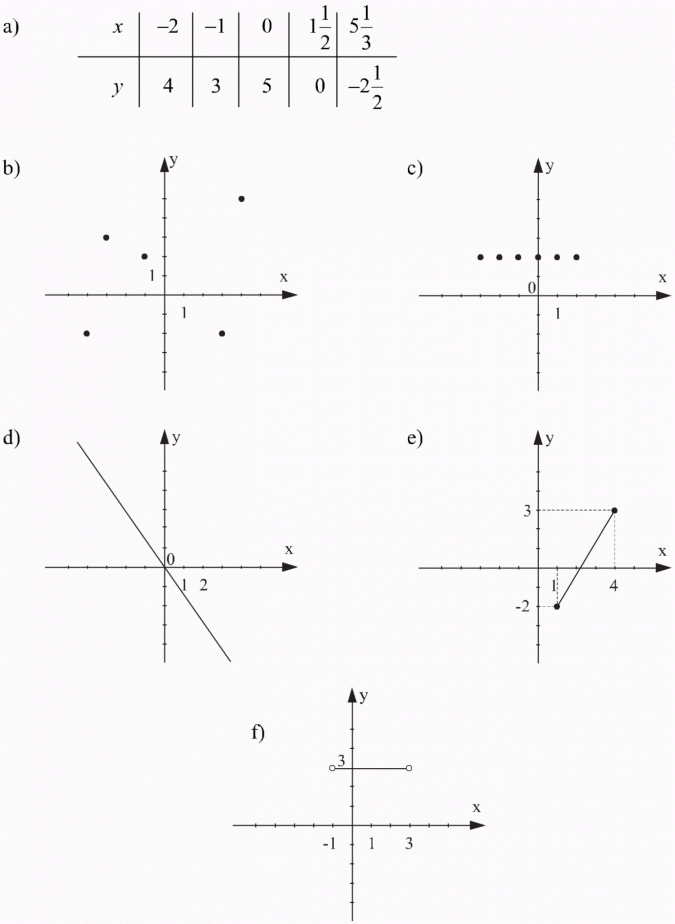
Dla każdej z tych funkcji odczytaj dziedzinę i zbiór wartości:
Rozwiązanie:
a) Dziedzina funkcji, to zbiór argumentów x (w tabelce w I wierszu umieszczamy argumenty, w II wierszu wartości funkcji dla tych argumentów).
Zbiór wartości funkcji odczytujemy na osi y:
Funkcja określona jest tabelką:
Zobaczmy, jak wyglądają wykresy funkcji określonych tym samym wzorem, ale o różnych dziedzinach.
Rozwiązanie:
Obliczam wartość funkcji y = x - 2 dla każdego argumentu, podstawiając do wzoru funkcji za x kolejno liczby z dziedziny funkcji. Otrzymuję wartość funkcji y, którą wpisuję do II wiersza w tabelce.
A zatem:
Każdej parze liczb odpowiada punkt w układzie współrzędnych.
Zbiór tych punktów jest wykresem naszej funkcji.
Wykresem funkcji jest zbiór tych wszystkich punktów płaszczyzny, których I współrzędna jest argumentem funkcji, a II współrzędna jest wartością funkcji dla tego argumentu.
Sporządzam tabelkę:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y = x - 2 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Obliczam wartość funkcji (czyli y) dla każdego argumentu x należącego do dziedziny funkcji.
W tym celu do wzoru funkcji y = x - 2 podstawiam kolejno za x liczby: 0, 1, 2, itd. i obliczam wartość y.
Wykresem jest zbiór punktów o współrzędnych (odczytuję z tabelki):
Zaznaczam otrzymane punkty w układzie współrzędnych
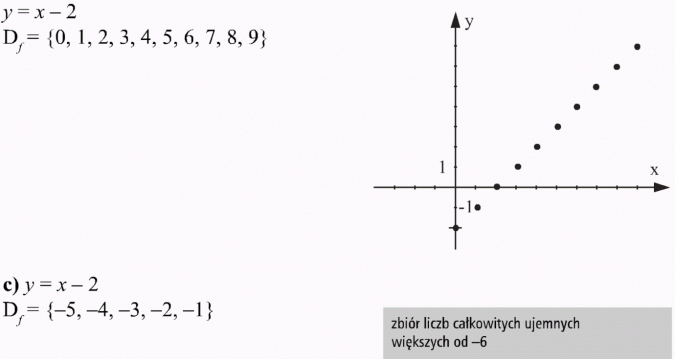
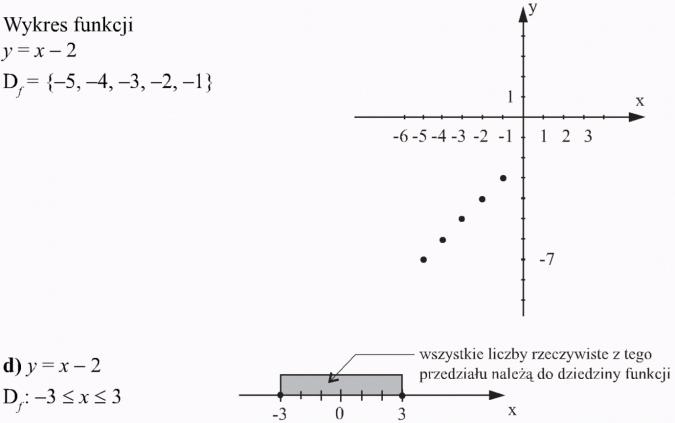
Sporządzam tabelkę:
| x | -5 | -4 | -3 | -2 | -1 |
| y = x - 2 | -7 | -6 | -5 | -4 | -3 |
Wykres funkcji jest zbiorem punktów o współrzędnych:
(-5, -7) (-4, -6) (-3, -5) (-2, -4) (-1, -3).
Zaznaczam je w układzie współrzędnych.
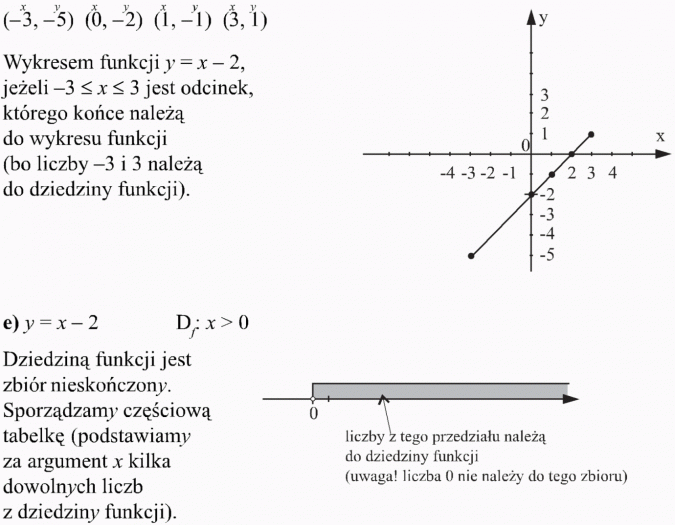
Dziedziną i zbiorem wartości funkcji jest nieskończony zbiór liczb, a zatem sporządzamy tylko częściową tabelkę (za argumenty x podstawiamy kilka liczb z dziedziny funkcji).
| x | -3 | 0 | 1 | 3 |
| y = x - 2 | -5 | -2 | -1 | 1 |
Obliczam wartość funkcji dla wybranych argumentów:
f(-3) = -3 - 2 = -5
f(0) = 0 - 2 = -2
f(1) = 1 - 2 = -1
f(3) = 3 - 2 = 1
Z tabelki odczytuję współrzędne punktów:
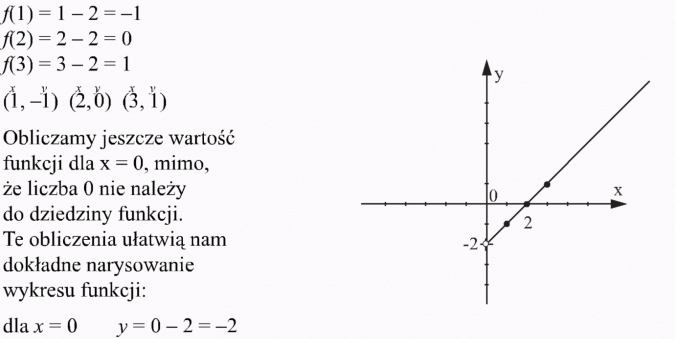
| x | 1 | 2 | 3 |
| y = x - 2 | -1 | 0 | 1 |
Obliczam wartości funkcji dla wybranych argumentów:
Wykresem funkcji y = x - 2 dla x > 0 będzie półprosta o początku w punkcie (0, -2) (ale uwaga! początek półprostej nie należy do wykresu funkcji, bo liczba 0 nie należy do dziedziny funkcji).
Dziedziną funkcji i zbiorem wartości funkcji jest nieskończony zbiór liczb rzeczywistych.
Sporządzamy częściową tabelkę:
| x | -1 | 0 | 2 |
| y = x - 2 | -3 | -2 | 0 |
Ważne!
Zauważ, że wykres funkcji zależy od dziedziny funkcji.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.