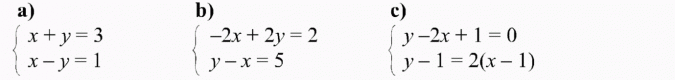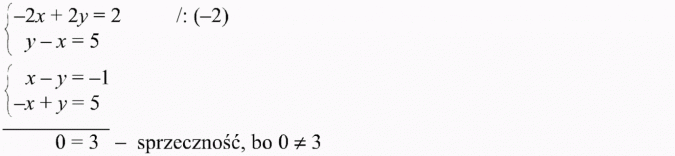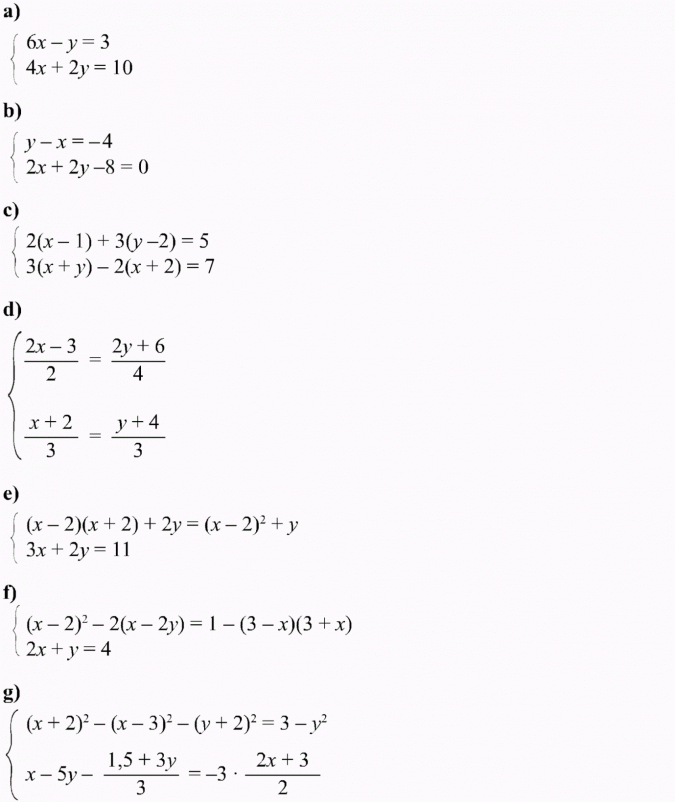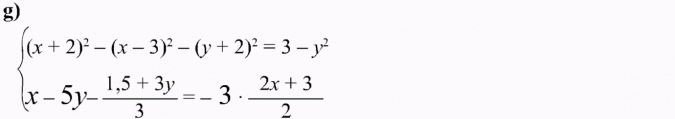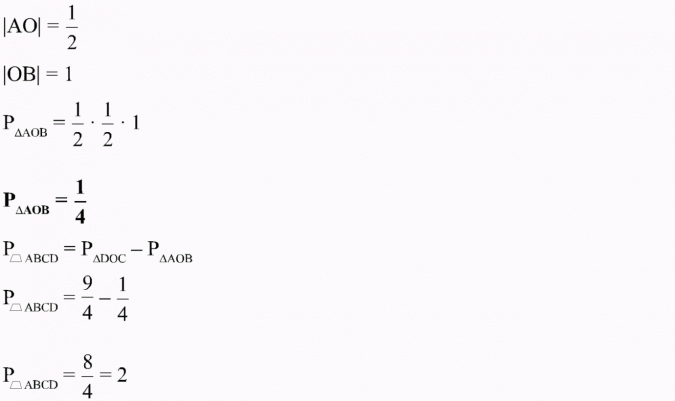zaprasza Cię do wspólnej nauki fiszek
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Przykład 1
Rozwiąż graficznie układ równań:
Sprawdzenie
Odp.: Para liczb x = 2 i y = 0 jest rozwiązaniem układu równań.
Graficzne rozwiązanie układu równań polega na:
- wyznaczeniu z każdego z równań y (czyli doprowadzeniu równania do postaci funkcji liniowej y = ax + b),
- narysowaniu wykresów obu funkcji w jednym układzie współrzędnych,
- odczytaniu jego rozwiązania.
Metoda graficzna rozwiązania układu równań nie zawsze jest skuteczna. Czasem trudno jest z wykresu odczytać rozwiązanie układu (np. proste przecinają się w punkcie o współrzędnych ułamkowych). Może się zdarzyć również, że punkt przecięcia nie mieści się na rysunku. Dlatego najczęściej rozwiązujemy układ równań algebraicznie i graficznie.
Rozwiąż algebraicznie i graficznie układ równań:
Rozwiązanie:
metoda algebraiczna:
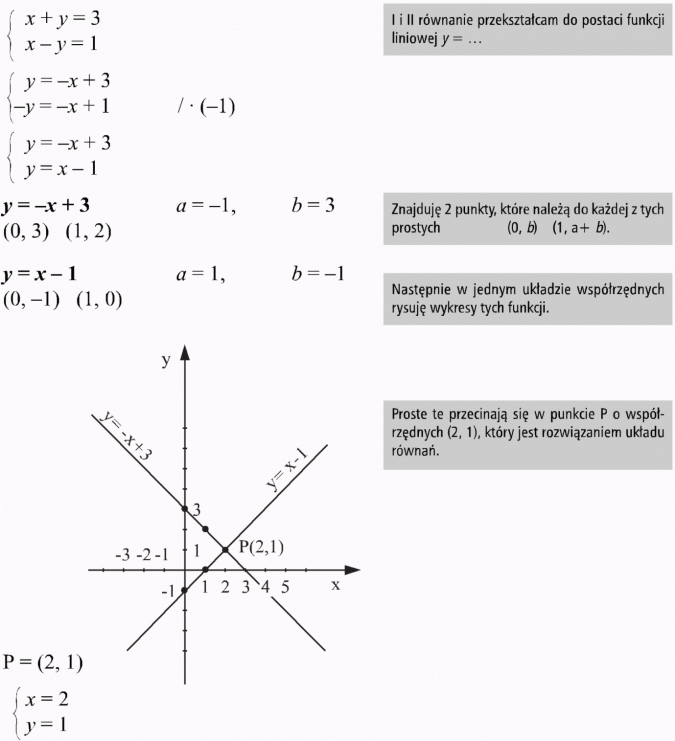
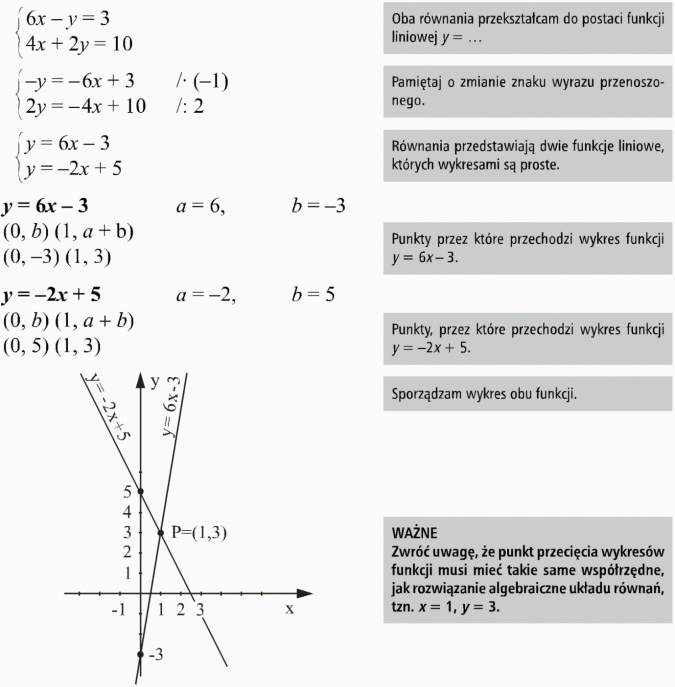
a)
metoda graficzna
Sprawdzenie:
Odp.: Para liczb x = 2 i y = 1 jest rozwiązaniem układu równań.
Rozwiązaniem układu równań jest jedna para liczb. Jest to układ oznaczony (układ równań niezależnych).
Wykresem oznaczonego układu równań są dwie proste przecinające się. Współrzędne punktu przecięcia się tych prostych są rozwiązaniem tego układu równań.
b)
rozwiązanie algebraiczne:
Jest to układ równań sprzecznych (układ sprzeczny). Taki układ równań nie ma rozwiązania. Zbiorem rozwiązań jest zbiór pusty.
rozwiązanie graficzne:
Wykresem układu równań sprzecznych są dwie proste równoległe.
Układ ten nie ma rozwiązania.
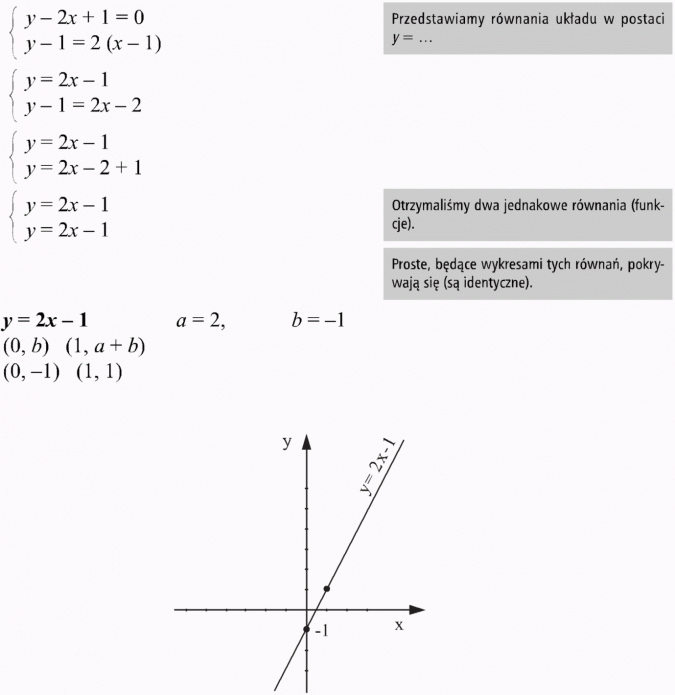
c)
metoda algebraiczna
Rozwiązaniem tego układu równań jest nieskończenie wiele par liczb.
rozwiązanie graficzne:
Odp.: Współrzędne każdego punktu tej prostej są rozwiązaniem układu równań. (Układ ma nieskończenie wiele rozwiązań.)
Układ równań, który posiada nieskończenie wiele rozwiązań nazywamy układem nieoznaczonym albo układem równań zależnych.
Wykresem nieoznaczonego układu równań są dwie proste pokrywające się.
Rozwiązanie:
rozwiązanie algebraiczne:
Odp.: Rozwiązaniem układu równań jest para liczb (1, 3).
rozwiązanie graficzne:
Odp.: Rozwiązaniem układu równań jest para liczb (1, 3).
rozwiązanie algebraiczne:
rozwiązanie graficzne:
rozwiązanie graficzne:
Odp.: Rozwiązaniem układu równań jest para liczb (2, 3).
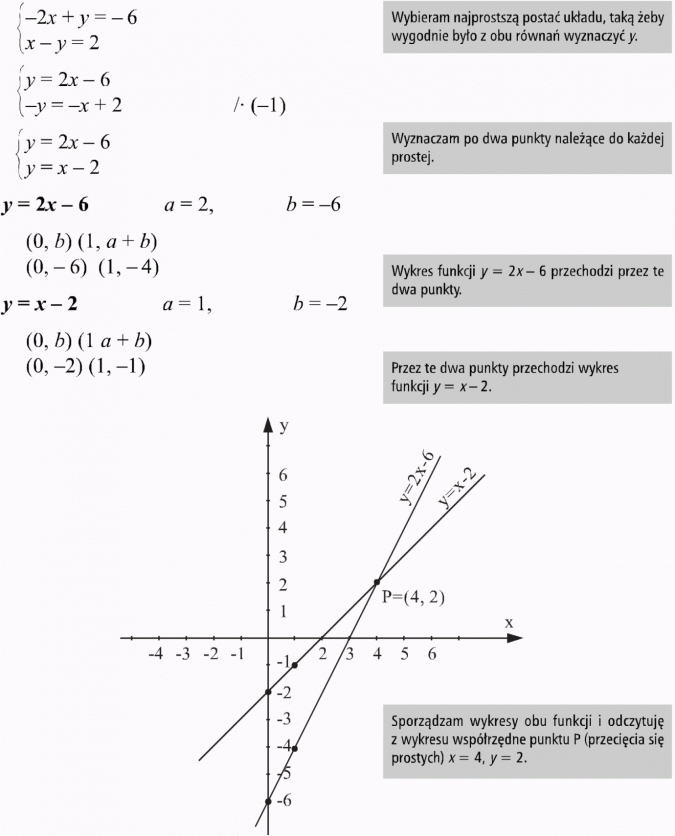
rozwiązanie algebraiczne:
rozwiązanie graficzne:
Odp.: Rozwiązaniem układu jest para liczb (4, 2).
rozwiązanie algebraiczne:
rozwiązanie graficzne:
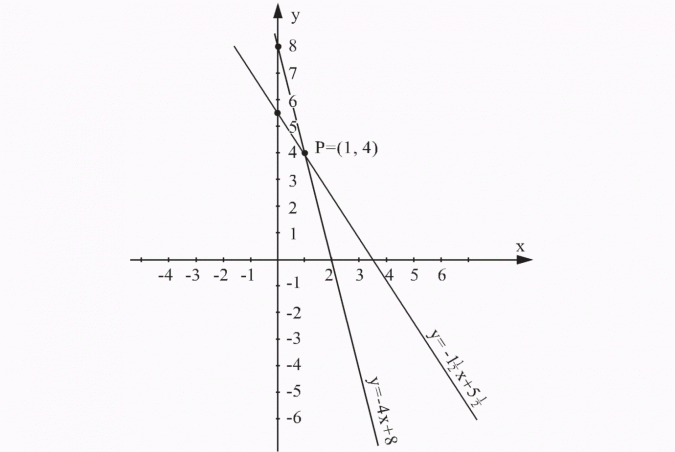
Następnie sporządzam wykresy obu funkcji i odczytuję z wykresów współrzędne punktu przecięcia się prostych.
Odp.: Rozwiązaniem układu równań jest para liczb (1, 4).
rozwiązanie algebraiczne:
metoda graficzna:
Odp.: Rozwiązaniem układu równań jest para liczb (2, 0).
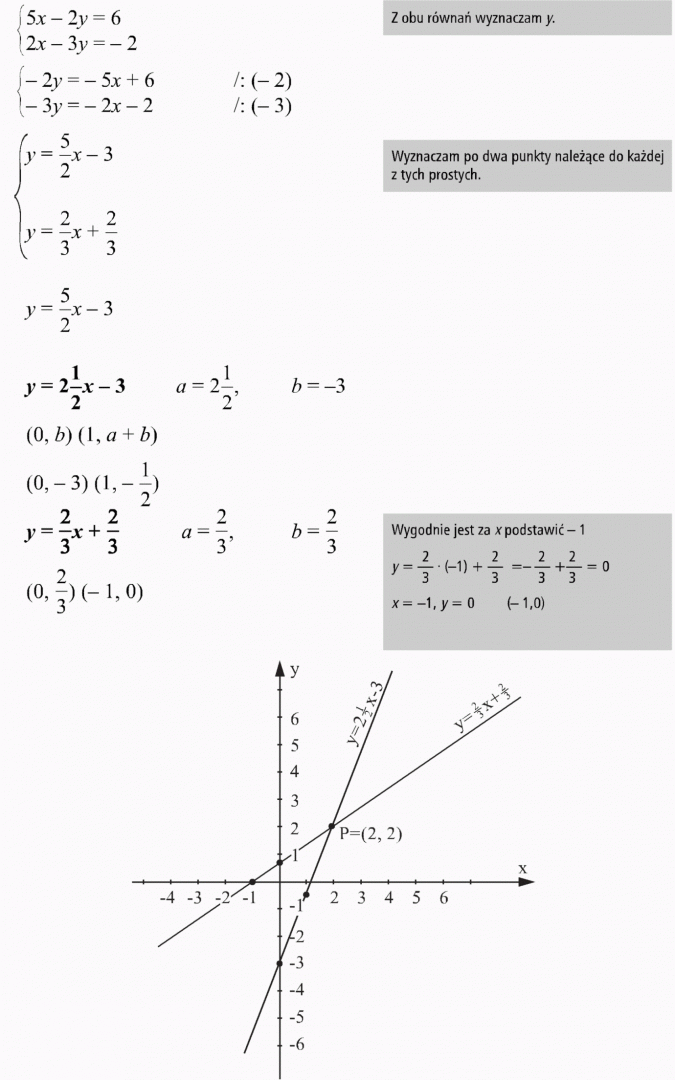
metoda algebraiczna:
rozwiązanie graficzne:
Odp.: Rozwiązaniem układu równań jest para liczb (2, 2).
Rozwiąż algebraicznie i graficznie układ równań:
Oblicz pole trójkąta ograniczonego wykresami tych równań i osią odciętych.
Rozwiązanie:
rozwiązanie algebraiczne układu równań:
Odp.: Rozwiązaniem układu jest para liczb (1, -3).
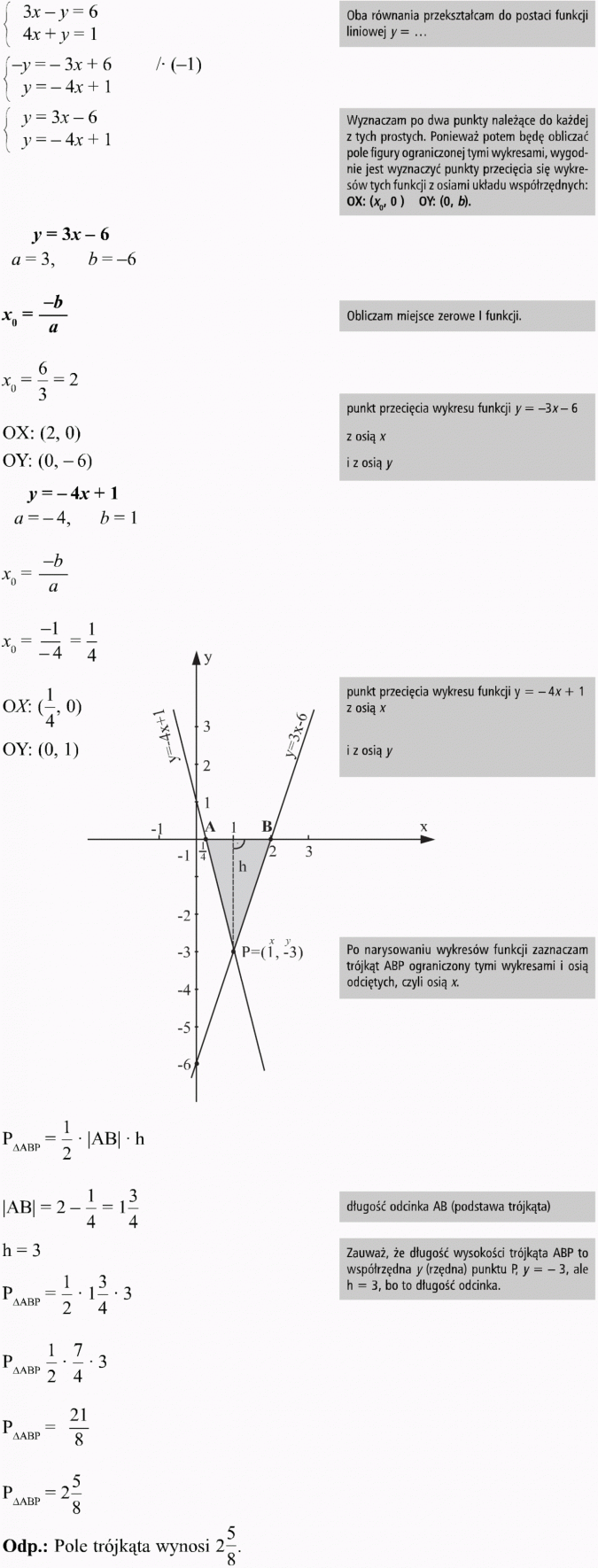
rozwiązanie graficzne:
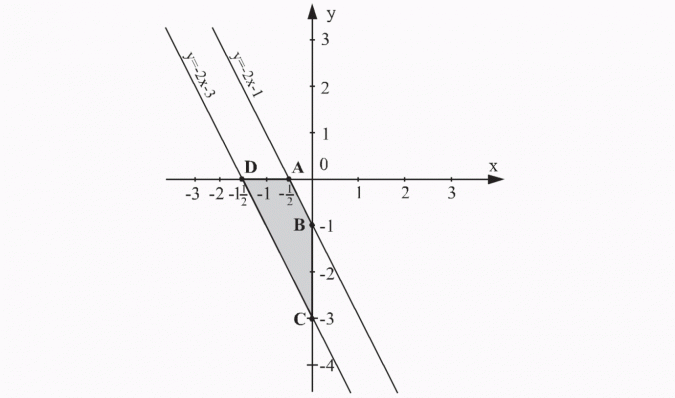
Narysuj w jednym układzie współrzędnych wykresy funkcji y = -2x - 1 i y = -2x -3 oraz oblicz pole figury ograniczonej tymi wykresami i osiami układu współrzędnych.
Rozwiązanie:
Po narysowaniu wykresów funkcji zaznaczamy figurę ograniczoną tymi wykresami i osiami układu współrzędnych.
Szukaną figurą jest trapez ABCD (AB || CD).
Aby obliczyć pole trapezu, trzeba znać długość podstaw |AB| i |CD| oraz wysokość trapezu.
Długość podstaw łatwo obliczyć (z twierdzenia Pitagorasa dla trójkątów AOB oraz DOC). Natomiast wysokość trapezu byłaby trudna do obliczenia.
Dlatego pole trapezu znajdziemy następująco: od pola trójkąta prostokątnego DOC odejmiemy pole trójkąta prostokątnego AOB. Czyli:
Pamiętamy, że pole trójkąta prostokątnego równe jest połowie iloczynu jego przyprostokątnych.
A zatem:
Z rysunku odczytujemy długość przyprostokątnych:
Z rysunku odczytujemy długość przyprostokątnych:
Odp.: Pole trapezu wynosi 2.
Jaka jest odległość punktu przecięcia wykresów funkcji y = 3x - 5 i y = -2x + 10 od początku układu współrzędnych?
Rozwiązanie:
W jednym układzie współrzędnych rysujemy wykresy obu funkcji.
Odległość punktu P od początku układu współrzędnych równa jest długości odcinka x.
Nietrudno zauważyć, że odcinek x jest przeciwprostokątną w trójkącie prostokątnym PBO (patrz rysunek).
A zatem długość odcinka x wyznaczymy z twierdzenia Pitagorasa.:
x2 = |OB|2 + |PB|2
x2 = 32 + 42
x2 = 9 + 16
x2 = 25
x = 5
Odp.: Odległość punktu P od początku układu współrzędnych wynosi 5.
Pogłębiaj wiedzę w temacie: Graficzna ilustracja układu równań
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.