Podstawowe równania i nierówności trygonometryczne

Zadanie 1

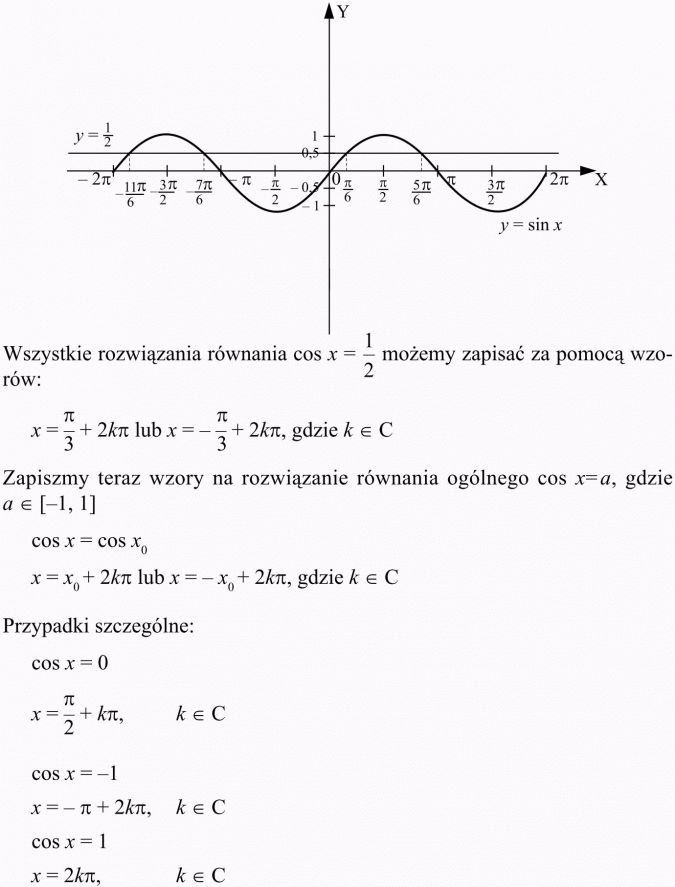
Bardzo łatwo zauważyć pewną zależność pomiędzy tymi rozwiązaniami. Mianowicie funkcja y = cos x jest parzysta, więc wykres jej funkcji jest symetryczny względem osi OY. Wystarczy znać jedno rozwiązanie, gdyż następne są jego całkowitymi wielokrotnościami oraz liczbami do niego przeciwnymi.

Podstawowe równania i nierówności trygonometryczne. Wszystkie rozwiązania równania cos x = 1/2 możemy zapisać za pomocą wzorów... Zapiszmy teraz wzory na rozwiązanie równania ogólnego cos x = a, gdzie... Przypadki szczególne.

Postępując analogicznie, możemy wyprowadzić wzory rozwiązań pozostałych funkcji trygonometrycznych.

Podstawowe równania i nierówności trygonometryczne. Rozwiązaniem równania tg... przy założeniu... są liczby postaci... Natomiast rozwiązaniem równania ctg... przy założeniu... są liczby postaci...

Zadanie 2

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Rozwiązanie. Jest to równanie elementarne (podstawowe), które nie wymaga przekształceń. Najpierw znajdujemy w tabelce taką wartość kąta x0, dla której sinus ma wartość... Kątem tym jest pi/4. Korzystamy ze wzorów...

Zadanie 3

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Jest to równanie elementarne, więc nie wymaga przekształceń. Po prawej stronie (w odróżnieniu od innych zadań) znajduje się liczba ujemna. Najpierw znajdujemy taką wartość kąta x0, dla której sinus ma wartość... nie znajdziemy w tabelce, ale jest tam... Sprawdzamy, dla jakiego kąta x0 sinus ma wartość... Jest nim... Szukany przez nas kąt ma wartość... a to dlatego, że sinus jest funkcją nieparzystą i sin... Znalezioną wartość kąta wstawiamy do wzoru na serie rozwiązań dla sinusa.

Zadanie 4

Rozwiąż równanie: 2 sin x = -1

Podstawowe równania i nierówności trygonometryczne. Równanie to trzeba przekształcić, dzieląc stronami przez 2. Dopiero równanie sin x = -1/2 jest elementarne. Najpierw szukamy takiego kąta x0, dla którego sinus ma wartość 1/2. Jest nim... Nasz kąt ma wartość..., ponieważ sinus jest funkcją nieparzystą, zatem... Znalezioną wartość kąta wstawiamy do wzoru rozwiązań sinusa.

Zadanie 5

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie. To równanie jest elementarne, mimo że zamiast x (tak jak w poprzednich zadaniach) mamy 5x. Tym na razie nie należy się przejmować. Szukamy takiego kąta x0, dla którego sinus ma wartość 1/2. Jest nim... Teraz należy uwzględnić 5x, pisząc ogólne wzory rozwiązań. Zamiast x piszemy 5x i znalezioną wartość x0 wstawiamy do wzorów. Aby znaleźć x, należy w obydwu równaniach obie strony podzielić przez 5. Tak będziemy postępować zawsze, ilekroś w temacie zadania pojawi się złożony argument (kąt), np.: 5x, (2x + 1) itd.

Zadanie 6

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie. Jest to równanie elementarne, mimo tego, że niewiadoma jest złożona (2x + 1). Szukamy kąta x0, dla którego sinus ma wartość... Teraz równania przekształcamy, z każdego wyliczając x. Znalezioną wartość podstawiamy do wzorów rozwiązań dla sinusa. Następnie równania przekształcamy tak, aby z każdego z nich wyliczyć x. Są to równania liniowe z jedną niewiadomą, zatem wystarczy niewiadomą pozostawić po lewej stronie, a wiadome (liczby) przenieść na prawą.

Zadanie 7

Rozwiąż równanie: 2 sin(x - 5) + 1 = 2.

Rozwiązanie:

Podstawowe równania i nierówności trygonometryczne. Równanie to wymaga prostych przekształceń, które prowadzą do uzyskania równania elementarnego. Od obydwu stron odejmujemy 1, następnie obie strony dzielimy przez 2. Uzyskujemy równanie elementarne. Teraz szukamy takiego kąta x0, dla któego sinus ma wartość 1/2. Jest nim... Wstawiamy znalezioną wartość... do wzorów rozwiązań, pamiętając, że zamiast x wpisujemy. Teraz z każdego równania wyliczamy x. Następnie uzyskane równania liniowe przekształcamy tak, aby uzyskać x. W tym celu w obydwu przypadkach przenosimy -5 na prawą stronę, zmieniając znak na przeciwny.

Zadanie 8

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Jest to równanie elementarne, nie wymaga przekształceń. Szukamy takiej wartości kąta x0, dla której cosinus ma wartość... Kątem tym jest... Teraz znalezione x0 wstawiamy do wzorów rozwiązań dla równania cos x = cos x0.

Zadanie 9

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Jest to równanie elementarne. Nie przejmuj się tym, że zamiast x jest x/2. Szukamy takiej wartości kąta x0, dla której cosinus ma wartość. Znalezioną wartość wstawiamy do wzorów rozwiązań, pamiętając o tym, że zamiast x piszemy x/2. Teraz z każdego równania wyliczamy x. Uzyskaliśmy dwa równania liniowe, z każdego z nich wyliczamy x, mnożąc równania obustronnie przez 2.

Zadanie 10

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Jest to równanie elementarne, nie wymaga przekształceń. Po prawej jest liczba ujemna, zatem należy postąpić w następujący sposób. Najpierw szukamy takiego kąta, dla którego cosinus przyjmuje wartość... Takim kątem jest... Ponieważ po prawej stronie równania mamy liczbę ujemną, należy znalezione... odjąć od... Wynika to ze wzorów redukcyjnych (tak postępujemy w przypadku cosinusa, bo cosinus jest funkcją parzystą i nie możemy postąpić tak, jak przy sinusie). Zgodne ze wzorami redukcyjnymi mamy... Teraz znalezioną wartość x0 wstawiamy do wzorów rozwiązań cosinusa.

Zadanie 11

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Rwnanie to nie jest elementarne, zatem należy skorzystać z faktu, że przypomina ono równanie typu a2 = 1/2, które rozwiązujemy, znajdując dwa pierwiastki. Naszym a jest cos x, stąd dwa równania. Uwalniamy mianownik od niewymierności. Rozwiązujemy teraz każde równanie z osobna... Równanie to jest elementarne. Szukamy takiej wartości kąta, dla której cosinus przyjmuje wartość... Aby znaleźć x0 należy posłużyć się wzorami redukcyjnymi. Znalezioną wartość x0 = 3/4 pi wstawiamy do wzorów rozwiązań. Równanie to jest elementarne. Szukamy takiej wartości kąta, dla której cosinus przyjmuje wartość... Znalezioną wartość x0 wstawiamy do wzorów.

Zadanie 12

Zadanie 13

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Jest to równanie elementarne. Szukamy takiego kąta, dla którego cotangens ma wartość... Wstawiamy tę wartość do wzoru rozwiązań dla cotangensa. Następnie rozwiązujemy równanie liniowe, mnożąc obie strony przez 4/3.

Zadanie 14

Rozwiąż równianie: tg 2x = -1

Podstawowe równania i nierówności trygonometryczne. Jest to równanie elementarne, szukamy takiej wartości kąta, dla której tangens przyjmuje wartość -1. Nie znajdziemy tej wartości w tabelce, ale dla... tangens ma wartość 1. Funkcja tangens jest nieparzysta... Znalezioną wartość x0 wstawiamy do wzoru rozwiązań tangensa. Następnie rozwiązujemy równanie liniowe.

Zadanie 15

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Szukamy takiej wartości kąta, dla której cotangens przyjmuje wartość... Funkcja cotangens jest również nieparzysta, czyli zachodzi warunek... Następnie do wzoru rozwiązań cotangensa wstawiamy za x0... i rozwiązujemy równanie liniowe.

Zadanie 16

Podstawowe równania i nierówności trygonometryczne. Rozwiąż równanie... Równanie przekształcamy, dzieląc obie strony przez 4. Uzyskujemy równanie postaci sin22x = 1/4. Równanie to rozkładamy na dwa. Każde z nich rozwiązujemy z osobna. Jest to równanie elementarne. Szukamy takiej wartości kąta, dla której sinus ma wartość -1/2. Jest nim... Znalezioną wartość kąta wstawiamy do wzorów rozwiązań sinusa, pamiętając o 2x. Następnie rozwiązujemy dwa równania liniowe. Szukamy kąta, dla którego sinus przyjmuje wartość 1/2. Jest nim... Znaleziony kąt wstawiamy do wzorów rozwiązań sinusa. Następnie rozwiązujemy dwa równania liniowe.

Zadanie 17

Podstawowe równania i nierówności trygonometryczne. Rozwiąż nierówność... Dzielimy nierówność stronami przez 2. Nierówność ta jest spełniona dla tych x, dla których wykres funkcji sinus leży poniżej prostej y = 1/2. Nalezy również wziąć pod uwagę to, że sin x = 1/2. Teraz rysujemy wykres funkcji y = sin x i y = 1/2 w przedziale... Patrzymy teraz na te części wykresu, które leżą poniżej prostej y = 1/2. Z osi OX odczytujemy przedziały spełniające nierówność.

Zadanie 18

Podstawowe równania i nierówności trygonometryczne. Rozwiąż nierówność... Rysujemy wykres funkcji sinus w przedziale... Pytamy teraz, kiedy wykres sinus leży nad prostą. Wynika to ze znaku nierówności. Rozwiązujemy też równanie pomocnicze. Na osi OX znajdujemy odpowiednie przedziały, których suma stanowi rozwiązanie nierówności. Rozwiązanie równania przydaje się przy ustalaniu punktów wspólnych prostej.

Zadanie 19

Podstawowe równania i nierówności trygonometryczne. Rozwiąż nierówność... Rysujemy wykres funkcji tangens w przedziale... Rysujemy wykres i rozwiązujemy pomocnicze równanie. Ten punkt należy do przedziału... Pytamy, kiedy wykres funkcji tangens leży pod prostą y... Po uwzględnieniu rozwiązania równania pomocniczego mamy...

Zadanie 20

Podstawowe równania i nierówności trygonometryczne. Rozwiąż nierówność... Rysujemy wykres funkcji cotangens w przedziale... Najpierw liczbę... uwolnijmy od niewymierności w mianowniku, mnożąc licznik i mianownik przez... Rozwiązujemy równanie pomocnicze. Ponieważ... wybieramy taką wartość spośród... która należy do tego przedziału. Pytamy, kiedy wykres funkcji cotangens leży nad prostą? Z wykresu odczytujemy przedział będący rozwiązaniem nierówności.

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Podstawowe równania i nierówności trygonometryczne