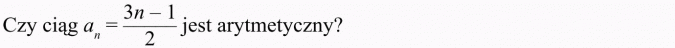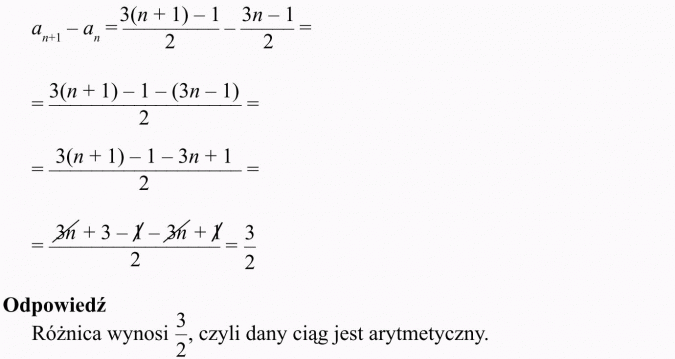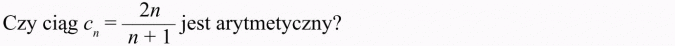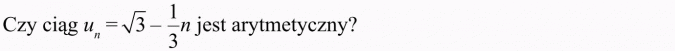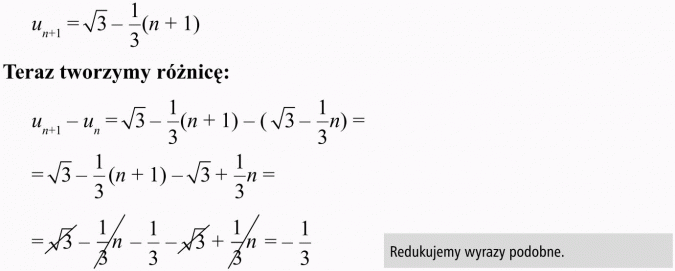Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Czy ciąg an = n jest arytmetyczny?
Rozwiązanie:
Należy sprawdzić, czy różnica an+1 - an jest stała (jest liczbą)
Utwórzmy tę różnicę:
Odpowiedź
Różnica wynosi r = 1, czyli ciąg an = n jest arytmetyczny.
Rozwiązanie:
Należy sprawdzić, czy różnica an+1 - an jest stała (jest liczbą)
Utwórzmy tę różnicę:
Rozwiązanie:
Należy sprawdzić, czy różnica an+1 - an jest stała (jest liczbą)
Utwórzmy tę różnicę:
Czy ciąg bn = n2 + 1 jest arytmetyczny?
Rozwiązanie:
Należy sprawdzić, czy różnica bn+1 - bn jest stała.
Utwórzmy:
Odpowiedź
Ciąg (bn) nie jest arytmetycznym.
Rozwiązanie:
Należy sprawdzić, czy różnica cn+1 - cn jest stała.
Utwórzmy:
Odpowiedź
Ciąg (cn) nie jest ciągiem arytmetycznym.
Rozwiązanie:
Należy sprawdzić, czy różnica un+1 - un jest stała.
Utwórzmy:
Odpowiedź
Różnica jest stała (jest liczbą), czyli ciąg jest arytmetyczny.
Wyznacz ciąg arytmetyczny, mając dane: a5 = 19 i a9 = 35.
Rozwiązanie:
Aby wyznaczyć ciąg arytmetyczny, trzeba znaleźć jego pierwszy wyraz (a1) oraz różnicę (r).
Otrzymaliśmy r = 4 i a1 = 3
Te dwie liczby wyznaczają jednoznacznie ciąg arytmetyczny.
Odpowiedź
r = 4, a1 = 3
Odpowiedź
a1 = 2, r = 3
Wyznacz ciąg arytmetyczny, mając dane a6 = 10 i a16 = 4.
Rozwiązanie:
Należy znaleźć pierwszy wyraz (a1) i różnicę (r).
Teraz znajdujemy Sn (sumę n pierwszych, kolejnych wyrazów ciągu arytmetycznego).
Wiedząc, że n = 50 (czyli 50 wyrazów ciągu), korzystamy ze wzoru
Wiedząc, że ciąg jest arytmetyczny i mając dane a1 = 3, r = 5, an = 57, znajdź: n, Sn.
Rozwiązanie:
Najpierw znajdujemy n (liczbę wyrazów ciągu arytmetycznego).
Teraz znajdujemy Sn (sumę n początkowych, kolejnych wyrazów ciągu). W tym celu posłużymy się wzorem.
Odpowiedź
n = 13, S13 = 351
Wiedząc, że cią jest arytmetyczny i mając dane r = 0,7, n = 21, an = 30, znajdź: a1, Sn.
Rozwiązanie:
Najpierw znajdujemy a1 (wartość pierwszego wyrazu ciągu).
W tym celu posłużymy się wzorem an = a1 + (n - 1)r.
Teraz znajdujemy Sn (sumę n początkowych, kolejnych wyrazów ciągu). W tym celu posłużymy się wzorem:
Odpowiedź
a1 = 16, S21 = 483
Wiedząc, że ciąg jest arytmetyczny i mając dane n = 21, an = 1, Sn = 0, znajdź: a1, r.
Rozwiązanie:
Najpierw znajdujemy a1 (wartość pierwszego wyrazu ciągu).
W tym celu posłużymy się wzorem:
Teraz znajdujemy r (różnicę ciągu arytmetycznego).
W tym celu posłużymy się wzorem an = a1 + (n - 1)r.
Przy kopaniu studni zapłacono za pierwszy metr głębokości 100 zł, natomiast za każdy następny o 50 zł więcej niż za poprzedni. Ile zapłacono za wykopanie 25-metrowej studni?
Rozwiązanie:
Odpowiedź
Koszt wykopania 25-metrowej studni wynosi 17 500 zł.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
