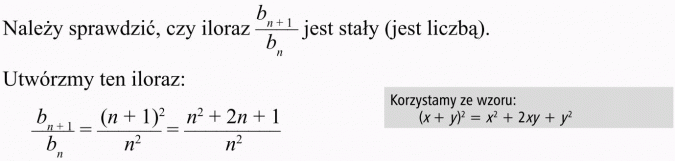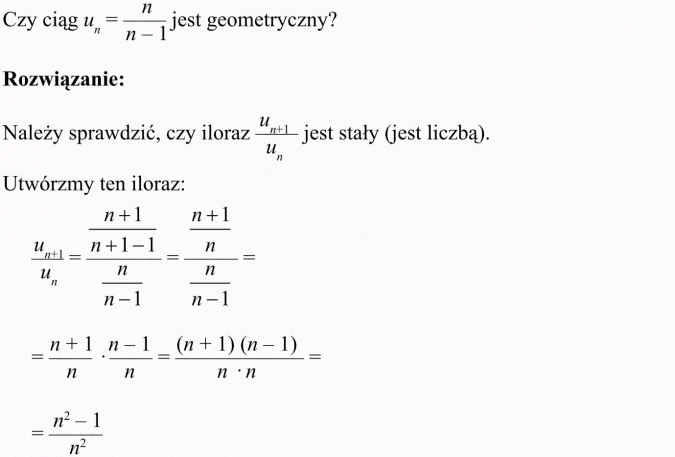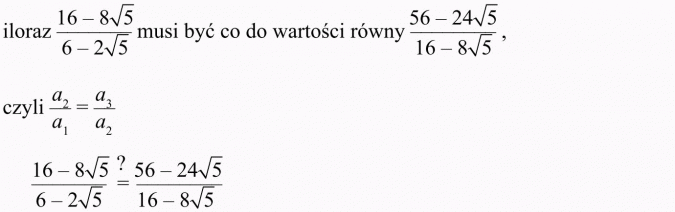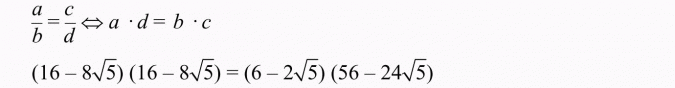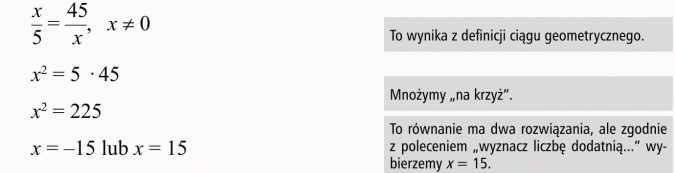Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Czy ciąg an = 2n jest geometryczny?
Rozwiązanie:
Odpowiedź
Iloraz wynosi 2, czyli ciąg an = 2n jest geometryczny
Czy ciąg bn = n2 jest geometryczny?
Rozwiązanie:
Iloraz nie jest stały, zależy od n, zmienia swoją wartość wraz ze zmianą n.
Odpowiedź
Ciąg bn = n2 nie jest geometryczny.
Iloraz nie jest stały, zależy od n, zmienia swoją wartość wraz ze zmianą n.
Odpowiedź
Wiedząc, że ciąg jest geometryczny i mając dane a1 = 2, q = 1,25, n = 4, znajdź: an, Sn.
Rozwiązanie:
Najpierw znajdujemy an, (n-ty wyraz ciągu geometrycznego).
Teraz znajdujemy Sn, (sumę n początkowych, kolejnych wyrazów ciągu geometrycznego).
Wiedząc, że ciąg jest geometryczny i mając dane a1 = 3, n = 5, an = 12, znajdź: q, Sn.
Rozwiązanie:
Najpierw znajdujemy q (iloraz ciągu geometrycznego).
Rozwiązanie:
Najpierw znajdujemy a1 (wartość pierwszego wyrazu ciągu).
W tym celu posłużymy się wzorem an = a1 · qn-1.
Odpowiedź
a1 = 729, Sn = 463
Wiedząc, że ciąg jest geometryczny i mając dane a1 = 2; q = 3; Sn = 6560, znajdź: n; an.
Rozwiązanie:
Najpierw znajdujemy n (liczbę wyrazów ciągu geometrycznego).
Teraz znajdujemy an (n-ty wyraz ciągu geometrycznego).
W tym celu posłużymy się wzorem an = a1 · qn-1.
Odpowiedź
n = 8, a8 = 4374
Rozwiązanie:
Korzystamy z definicji ciągu geometrycznego, z której wynika, że iloraz dowolnego wyrazu i wyrazu bezpośrednio poprzedzającego jest wielkością stałą dla danego ciągu, czyli:
Tę równość spróbujemy sprawdzić, wykonując mnożenie „na krzyż”.
Teraz wykonujemy zaznaczone działania po lewej i prawej stronie równania:
To warto zapamiętać!
Trzy liczby x, y, z (różne od zera) tworzą ciąg geometryczny, gdy kwadrat środkowej liczby równa się iloczynowi skrajnych, czyli y2 = x · z.
Trzy liczby, których iloczyn wynosi 64, tworzą ciąg geometryczny. Te same liczby tworzą także ciąg arytmetyczny. Jakie to liczby?
Rozwiązanie:
Oznaczamy poszukiwane liczby x, y, z.
Teraz każde zdanie z treści zadania spróbujemy zastąpić równaniem.
Odpowiedź
Te liczby to: 4, 4, 4. (Tworzą one ciąg geometryczny stały).
Między liczby 5 i 45 wstaw liczbę x tak, by liczby 5, x, 45 tworzyły ciąg geometryczny.
Rozwiązanie:
Dane są cztery liczby. Trzy pierwsze z nich tworzą ciąg geometryczny, zaś trzy ostatnie ciąg arytmetyczny. Suma liczb skrajnych równa się 14, suma środkowych równa się 12. Znajdź te liczby.
Rozwiązanie:
Oznaczamy szukane liczby x, y, z, t.
Każde zdanie z treści zadania przetwarzamy na równanie.
Powstał układ równań, który należy rozwiązać:
Znalezione wartości y podstawiamy do równań:
Odpowiedź
Dane cztery liczby tworzą dwa ciągi geometryczne postaci: (2, 4, 8, 12) lub (12,5; 7,5; 4,5; 1,5).
Wyznacz liczbę dodatnią x taką, aby ciąg 5, x, 45 był ciągiem geometrycznym.
Rozwiązanie:
5, x, 45 jest geometryczny, gdy iloraz dowolnego wyrazu i wyrazu bezpośrednio go poprzedzającego jest stały (jest liczbą), zatem:
Odpowiedź
x = 15, ciąg ma postać (5, 15, 45).
Hanka kupiła trzy książki, za które zapłaciła łącznie 61 zł. Ceny tych książek tworzą ciąg geometryczny. Za pierwszą i drugą zapłaciła o 11 zł więcej niż za trzecią. Ile Hanka zapłacila za każdą z książek?
Odpowiedź
Hanka zapłaciła za ksiązki 16 zł, 20 zł, 25 zł.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
