Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Przykład 1
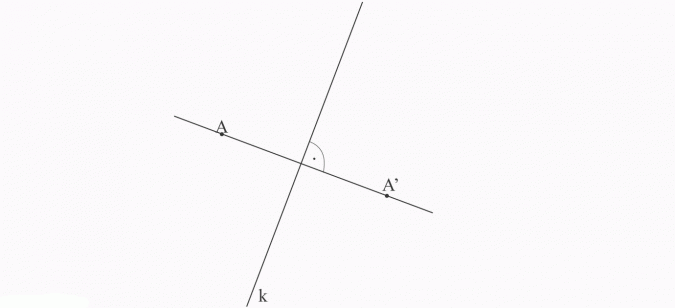
Znajdź punkt A’ symetryczny do punktu A względem prostej k.
Opis:
1) rysuję prostą k i zaznaczam punkt A nie leżący na tej prostej,
2) rysuję (przy pomocy ekierki) prostą prostopadłą do prostej k przechodzącą przez punkt A,
3) na tej prostej znajduję punkt A’ (posługuję się cyrklem lub linijką z podziałką).
Przykład 2
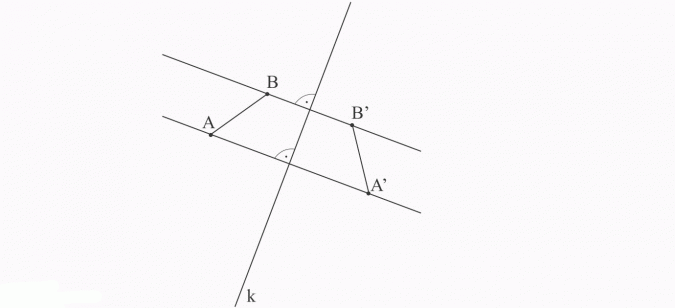
Narysuj odcinek symetryczny do odcinka AB względem prostej k.
Opis:
1) rysuję odcinek AB i prostą k,
2) znajduję obraz punktu A oraz punktu B w symetrii względem prostej k (postępując dokładnie tak, jak w przykładzie 1),
3) łączę punkty A’ i B’, otrzymuję odcinek A’B’ symetryczny do odcinka AB względem prostej k.
Punkty A i A’ są symetryczne do siebie względem punktu S, jeżeli punkt S jest środkiem odcinka AA’.
|AS| = |A’S|
Przykład 1
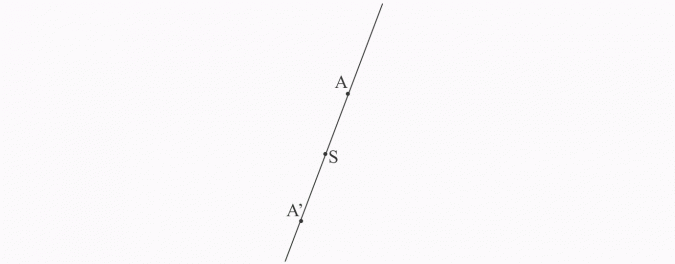
Narysuj odcinek symetryczny do odcinka AB względem punktu S.
Opis:
1) rysuję odcinek AB i zaznaczam punkt S nie należący do odcinka,
2) przez punkty A i S prowadzę prostą,
3) punkt A’ leży po drugiej stronie punktu S w tej samej odległości co punkt A, więc |AS| = |A’S| (punkt S jest środkiem odcinka AA’),
4) podobnie znajduję punkt B’, pamiętając, że dwa punkty symetryczne względem punktu S leżą na prostej przechodzącej przez punkt S, po przeciwnych stronach punktu S i w równych od niego odległościach.
Narysuj trójkąt symetryczny do danego trójkąta ABC względem prostej k przecinającej boki trójkąta.
Opis:
1) rysuję trójkąt ABC i prostą k przecinającą boki trójkąta,
2) rysuję prostą prostopadłą do prostej k przechodzącą przez punkt A,
3) znajduję punkt A’ (obraz punktu A) - postępując tak jak w przykładzie 1,
4) podobnie znajduję obraz punktu B oraz punktu C (pamiętając o trzech warunkach jakie spełniają punkty symetryczne: leżą na prostej prostopadłej, leżą po przeciwnych stronach i w równych odległościach od prostej k).
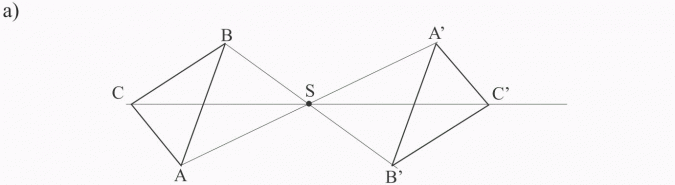
Narysuj trójkąt ABC, a następnie wykreśl trójkąt A’B’C’ symetryczny do trójkąta ABC względem punktu S leżącego:
a) na zewnątrz trójkąta ABC
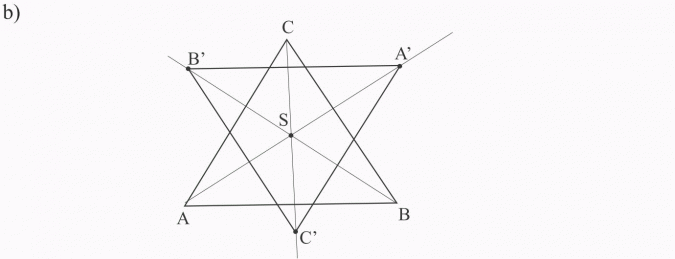
b) wewnątrz trójkąta ABC
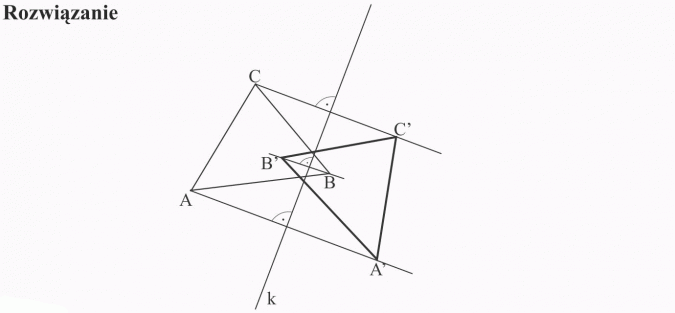
Rozwiązanie
Opis:
1) znajduję punkty symetryczne do punktów, A, B, C (wierzchołków trójkąta) względem punktu S, postępując dokładnie tak, jak w przykładzie 1,
2) łączę odcinkami punkty A’, B’, C’. Otrzymuję trójkąt A’B’C’ symetryczny do trójkąta ABC względem punktu S.
Zauważ, że:
Odcinki symetryczne do siebie względem punktu mają jednakową długość i są równoległe.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.