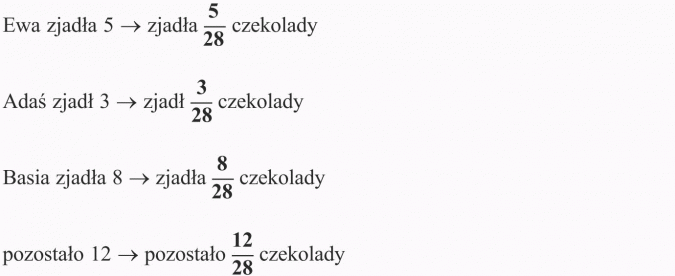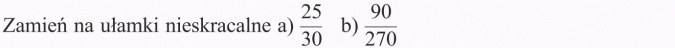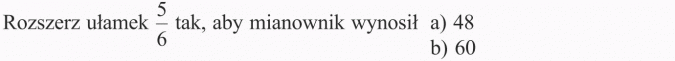Ułamek jako część całości (na poziomie ucznia klasy 4)

Ułamki zwykłe są zapisem wielkości będących częścią jedności (całości).

Przykład 1

Ułamek jako część całości. Czyt. jedna druga, jedna trzecia, trzy szóste, trzy dziesiąte, pięć ósmych. Licznik, kreska ułamkowa, mianownik. Czyt. trzy czwarte. Mianownik 4 - ponieważ na 4 równe części podzielono kwadrat. Licznik 3 - ponieważ 3 części zostały zamalowane. Uwaga: Ten rysunek nie ilustruje ułamka 3/4, ponieważ 4 części, na które podzielono kwadrat, nie są równe.

Zadanie 1

Czekolada składała się z 28 kostek. Ewa zjadła 5, Adaś 3, a Basia 8 kostek. Jaką część czekolady zjadło każde z dzieci? Jaka część pozostała?

Rozwiązanie

Rysunek ułatwi rozwiązanie

Ułamek jako część całości. Kostki, które zjadła Ewa, Kostki, które zjadł Adaś, Kostki, które zjadła Basia.

Czekolada składała się z 28 kostek, więc mianownik ułamka wynosi 28. Ilość kostek, którą zjadło każde z dzieci to licznik.

Ułamek jako część całości. Ewa zjadła 5 - zjadła 5/28 czekolady. Adaś zjadł 3 - zjadł 3/28 czekolady. Basia zjadła 8 - zjadła 8/28 czekolady. Pozostało 12 - pozostało 12/28 czekolady.

Zadanie 2

Na osi liczbowej zaznacz 1/6, 4/6 i 5/6.

Rozwiązanie

Aby zaznaczyć ułamki o mianowniku 6, musisz podzielić odcinek od 0 do 1 na 6 równych części. Zatem odcinek jednostkowy musi mieć długość łatwo podzielną przez 6 (6 cm, 12 cm, 6 kratek itp.)

Ułamek jako część całości. Odcinek od 0 do pierwszej kratki pionowej to 1/6, od 0 do następnej to 2/6 itd.

Zadanie 3

Jaką częścią kilograma jest 1 gram, a jaką 18 gramów?

Rozwiązanie

1 kg = 1000 g

1 kilogram został podzielony na 1000 jednakowych części (gramów), czyli mianownik ułamka wynosi 1000

1 gram to jedna część z tego tysiąca, czyli licznik wynosi 1

Ułamek jako część całości. 1 g = 1/1000 kg

Podobnie 18 g to 18 części z 1000 g

Ułamek jako część całości. 18 g = 18/1000 kg

Określenie „całość”, którą dzielisz „na równe części” nie zawsze musi oznaczać tabliczkę czekolady, kwadrat czy koło. Za całość można uważać zbiór elementów (niekoniecznie jednakowych), których ilość będzie stanowiła mianownik, a cecha, która łączy kilka z nich - licznik ułamka.

Przykład 2

Ułamek jako część całości. Całość składa się z 7 kropek (różnej wielkości), 3 spośród nich są czarne, 4 białe. Ułamek czarnych kropek to 3/7. Ułamek białych kropek to 4/7. Całość to 5 figur geometrycznych. 3 spośród nich to wielokąty, 2 to koła. Koła stanowią 2/5 figur, wielokąty 3/5 figur.

Zadanie 4

W klasie IV a jest 8 dziewczynek i 17 chłopców. Jaką część klasy stanowią dziewczynki?

Rozwiązanie

Liczba uczniów w klasie IV a (chłopców i dziewczynek) będzie mianownikiem ułamka:

8 + 17 = 25

Liczba dziewczynek (8) to licznik ułamka.

Ułamek jako część całości. Liczba dziewczynek, liczba wszystkich uczniów.

Odp.:

Ułamek jako część całości. Dziewczynki stanowią 8/25 klasy IV a.

Czy różnie wyglądające ułamki mogą przedstawiać taką samą część? Odpowiedź brzmi: TAK!

Przykład 3

Ułamek jako część całości. Ułamek 1/2 rozszerzyłam przez 4. Ułamek 1/3 rozszerzyłam przez 2. Ułamek 2/3 rozszerzyłam przez 3.

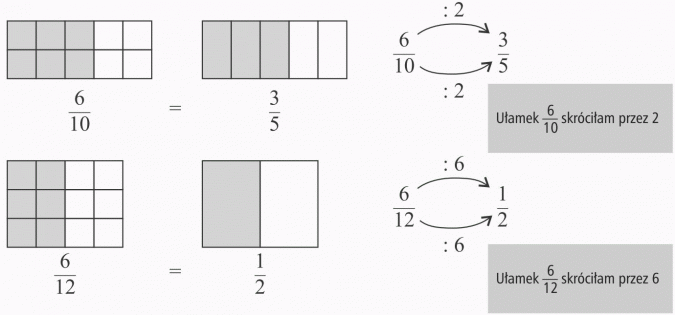
Rozszerzyć ułamek znaczy pomnożyć licznik i mianownik przez tę samą liczbę (oczywiście różną od zera). TAKI UŁAMEK NIE ZMIENIA SWOJEJ WARTOŚCI.

Możesz postąpić odwrotnie czyli skrócić ułamek.

Przykład 4

Ułamek jako część całości. Ułamek 6/10 skróciłam przez 2. Ułamek 6/12 skróciłam przez 6.

Skrócić ułamek znaczy podzielić licznik i mianownik przez tę samą liczbę (różna od zera). UŁAMEK NIE ZMIENI SWOJEJ WARTOŚCI.

Możliwość skrócenia ułamka zależy od tego, czy licznik i mianownik mają wspólny dzielnik.

Jeżeli licznik i mianownik nie mają wspólnego dzielnika, to jest to ułamek nieskracalny.

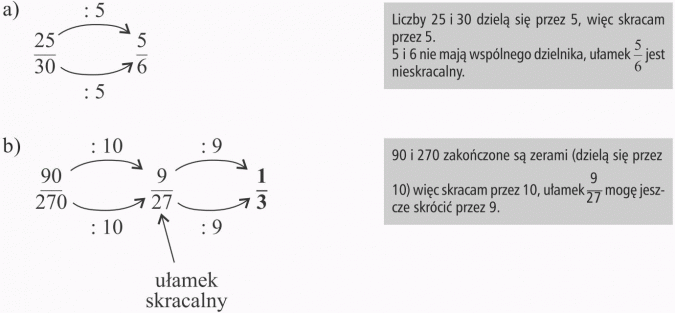
Przykład 5

Ułamek jako część całości. Dzielniki licznika, dzielniki mianownika.

Poza liczbą 1 nie ma wspólnego dzielnika

Ułamek jako część całości. Ułamek nieskracalny. Dzielniki licznika, dzielniki mianownika.

brak wspólnego dzielnika → ułamek nieskracalny

Zadanie 5

Ułamek jako część całości. Zamień na ułamki nieskracalne.

Rozwiązanie

Ułamek jako część całości. Liczby 25 i 30 dzielą się przez 5, więc skracam przez 5. 5 i 6 nie mają wspólnego dzielnika, ułamek 5/6 jest nieskracalny. 90 i 270 zakończone są zerami (dzielą się przez 10), więc skracam przez 10, ułamek 9/27 mogę jeszcze skrócić przez 9. Ułamek skracalny.

UWAGA: Skracanie można przeprowadzić stopniowo lub jednorazowo, znając największy wspólny dzielnik.

Ułamek jako część całości. Największym wspólnym dzielnikiem liczb 90 i 270 jest 90, więc skracam przez 90.

Zadanie 6

Ułamek jako część całości. Rozszerz ułamek 5/6 tak, aby mianownik wynosil 48 i 60.

Rozwiązanie

Ułamek jako część całości. Aby dowiedzieć się, przez ile rozszerzyć ułamek 5/6, dzielisz mianownik 48 przez obecny mianownik (6). Należy rozszerzyć ułamek przez 8. Postępujesz tak samo, jak poprzednio. Należy rozszerzyć ułamek przez 10.

Zadanie 7

Ułamek jako część całości. Ułamek 5/6 rozszerz tak, aby licznik wynosił 55. Tym razem aby ustalić, przez ile rozszerzyć ułamek, dzielisz licznik 55 przez obecny licznik (5). 55 : 5 = 11 - należy rozszerzyć ułamek przez 11.

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Ułamek jako część całości (na poziomie ucznia klasy 4)