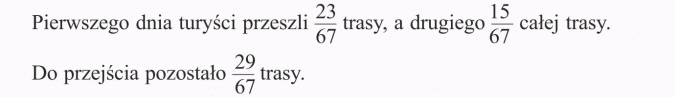Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Jak zapewne pamiętasz z poprzednich klas, ułamki zwykłe to liczby zapisane w postaci:
Licznik może być dowolną liczbą naturalną, natomiast mianownik musi być liczbą różną od zera.
Przykłady
Jaką częścią
a) godziny jest 1 minuta;
b) tygodnia jest weekend;
c) metra jest 1 decymetr;
d) kilograma jest 13 gramów.
Rozwiązanie:
Trasa wycieczki miała długość 67 km. Turyści przeszli pierwszego dnia 23 km, a drugiego tylko 15 km. Jaką część trasy pokonali pierwszego, a jaką drugiego dnia? Jaka część trasy pozostała do przejścia?
Rozwiązanie:
Odpowiedź:
W zawodach sportowych brali udział uczniowie klas: Va, Vb i Vc. W tabelce zostały podane składy reprezentacji poszczególnych klas:
| Va | Vb | Vc | |
|---|---|---|---|
| liczba dziewcząt | 5 | 7 | 9 |
| liczba chłopców | 3 | 2 | 5 |
a) Jaką część uczestników stanowiły dziewczęta, a jaką chłopcy?
b) Jaką część chłopców stanowili chłopcy z klasy Va?
Rozwiązanie:
Odpowiedź:
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.