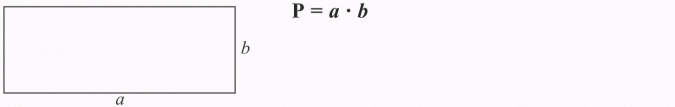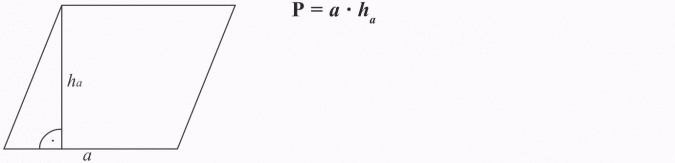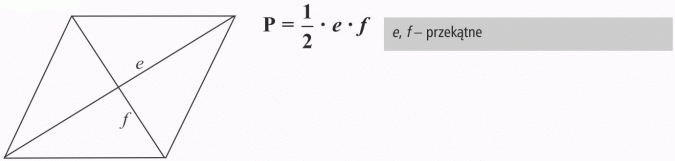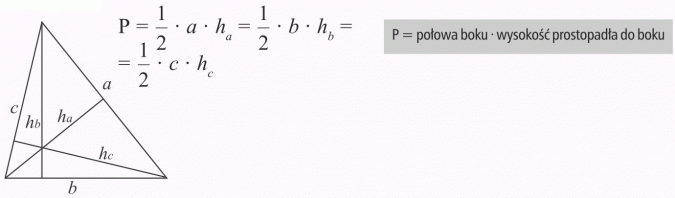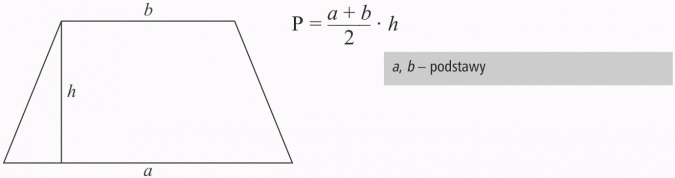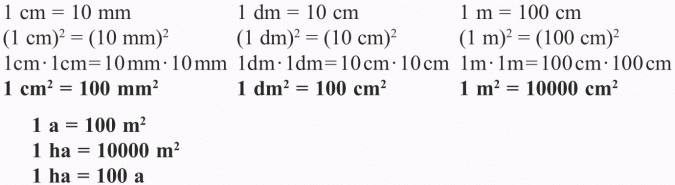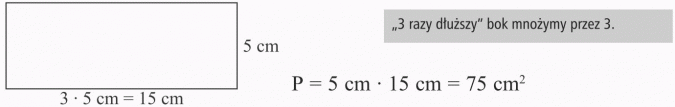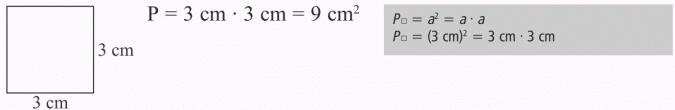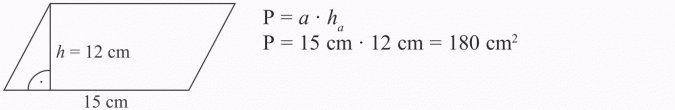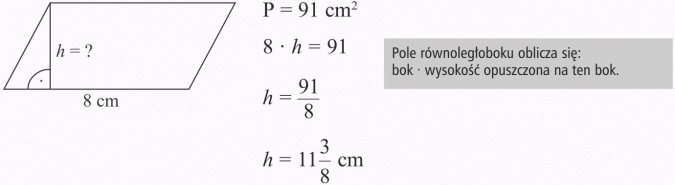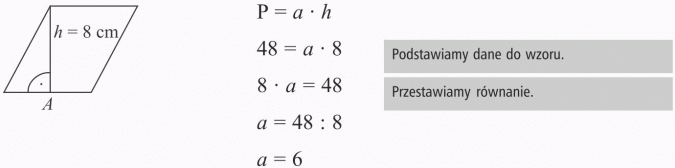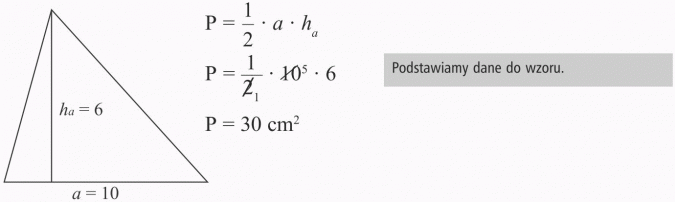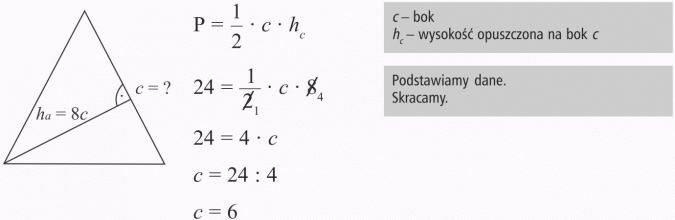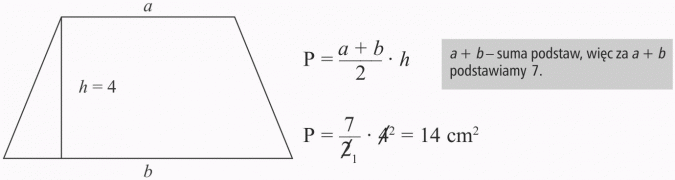Pola figur (na poziomie ucznia klasy 6)

PROSTOKĄT

KWADRAT

RÓWNOLEGŁOBOK

ROMB

TRÓJKĄT

TRAPEZ

Jednostki pola:

Pola figur. 1 cm = 10 mm. (1 cm)2 = (10 mm)2. 1 cm x 1 cm = 10 mm x 10 mm. 1 cm2 = 100 mm2. 1 dm = 10 cm. (1 dm)2 = (10 cm)2. 1 dm x 1 dm = 10 cm x 10 cm. 1 dm2 = 100 cm2. 1 m = 100 cm. (1 m)2 = (100 cm)2. 1m x 1m = 100cm x 100 cm. 1 m2 = 10000 cm2. 1 a = 100 m2. 1 ha = 10000 m2. 1 ha = 100 a.

Zadanie 1

Jeden z boków prostokąta ma 5 cm, a drugi jest 3 razy dłuższy. Oblicz pole prostokąta.

Pola figur. 3 razy dłuższy bok mnożymy przez 3.

Zadanie 2

Oblicz pole kwadratu, którego obwód wynosi 6 dm.

Pola figur. Obwód. Skracamy ułamek. Wyciągamy całości.

Zadanie 3

Oblicz obwód kwadratu, którego pole jest równe 25 cm².

P = a · a

a · a = 25 cm²

a = 5

Obwód = 4 · 5 cm = 20 cm

Zadanie 4

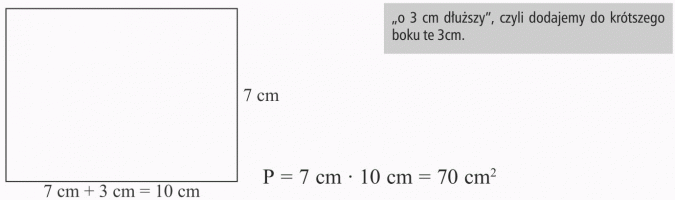
Jeden bok prostokąta ma 7 cm, a drugi jest o 3 cm dłuższy. Oblicz pole prostokąta.

Pola figur. O 3 cm dłuższy, czyli dodajemy do krótszego boku te 3 cm.

Zadanie 5

Oblicz pole kwadratu o boku 3 cm.

Zadanie 6

Łazienka ma kształt prostokąta o wymiarach 4,5 m x 2,5 m. Ile płytek terakoty w kształcie kwadratu o boku 10 cm potrzeba na wyłożenie podłogi w tej łazience?

Pola figur. Obliczamy pole powierzchni podłogi w tej łazience. Obliczamy pole płytki, ale najpierw zamieniamy 10 cm na część metra. Obliczamy, ile takich kwadratowych płytek zmieści się na podłodze. Przesuwamy przecinek w prawo w obu liczbach o dwa miejsca.

Odpowiedź:

Aby ułożyć podłogę w łazience, należy kupić 1125 płytek.

Zadanie 7

Oblicz pole równoległoboku, którego bok ma długość 15 cm, a wysokość opuszczona na ten bok wynosi 12 cm.

Zadanie 8

Pola figur. Pole równoległoboku oblicza się: bok x wysokość opuszczona na ten bok.

Odpowiedź:

Pola figur. Wysokość opuszczona na bok równy 8 cm ma 11 3/8 cm.

Zadanie 9

Długości boków równoległoboku są równe: 16 cm i 8 cm. Wysokość opuszczona na krótszy bok ma 10 cm. Jaką długość ma wysokość opuszczona na dłuższy bok?

Pola figur. Obliczyliśmy pole, bo dany był bok i wysokość opuszczona na ten bok.

Odpowiedź:

Wysokość opuszczona na dłuższy bok ma 5 cm.

Zadanie 10

Jedna przekątna rombu ma długość 12 cm, a druga jest 3 razy dłuższa. Oblicz pole rombu.

Pola figur. Przekątne rombu. Bo jest 3 razy dłuższa.

Odpowiedź:

Pole rombu wynosi 216 cm².

Zadanie 11

Pole rombu jest równe 84 cm². Jedna z jego przekątnych ma długość 12 cm. Jaką długość ma druga przekątna?

Pola figur. Podstawiamy dane do wzoru. Można przestawić strony.

Odpowiedź:

Druga przekątna ma 14 cm.

Zadanie 12

Pole rombu wynosi 48 cm², wysokość rombu 8 cm. Oblicz bok rombu.

Pola figur. Podstawiamy dane do wzoru. Przestawiamy równanie.

Odpowiedź:

Pole rombu ma 6 cm.

Zadanie 13

Podstawa trójkąta wynosi 10 cm, a wysokość opuszczona na ten bok 6 cm. Oblicz pole trójkąta.

Zadanie 14

Pole trójkąta wynosi 15 cm², jeden z jego boków jest równy 5 cm. Oblicz wysokość opuszczoną na ten bok.

Pola figur. Podstawiamy do wzoru. Mnożymy 1/2 x 5 = 5/2. Zmieniamy strony. Dzielimy przez 5/2. Znak : zastępujemy mnożeniem przez odwrotność drugiej liczby. Skracamy.

Zadanie 15

Pole trójkąta wynosi 24 cm², a jedna z jego wysokości jest równa 8 cm. Oblicz długość boku, któremu odpowiada ta wysokość.

Pola figur. Bok. Wysokość opuszczona na bok c. Podstawiamy dane. Skracamy.

Odpowiedź:

Szukany bok ma 6 cm.

Zadanie 16

Pole trójkąta prostokątnego jest równe 5 cm². Jedna przyprostokątna ma długość 2 cm. Znajdź długość drugiej przyprostokątnej.

Pola figur. W trójkącie prostokątnym przyprostokątna jest wysokością, bo jest prostopadła do boku. Podstawiamy dane. Obliczylismy długość ha, która jest przyprostokątną.

Odpowiedź:

Druga przyprostokątna ma 5 cm.

Zadanie 17

Wysokość trójkąta jest 3 razy dłuższa od boku, na który jest opuszczona i wynosi 12 cm. Jakie pole ma ten trójkąt?

Pola figur. Wysokość jest 3 razy dłuższa od boku, więc bok jest 3 razy krótszy od wysokości. Podstawiamy dane do wzoru.

Odpowiedź:

Ten trójkąt ma pole równe 24 cm².

Zadanie 18

W trapezie jedna z podstaw ma długość 26 cm, druga podstawa jest dwa razy od niej krótsza. Wysokość trapezu jest równa 12 cm. Oblicz pole tego trapezu.

Pola figur. Podstawy (odcinki równoległe). 2 razy mniejsza - dzielimy przez 2. Podstawiamy do wzoru.

Odpowiedź:

Pole trapezu wynosi 234 cm².

Zadanie 19

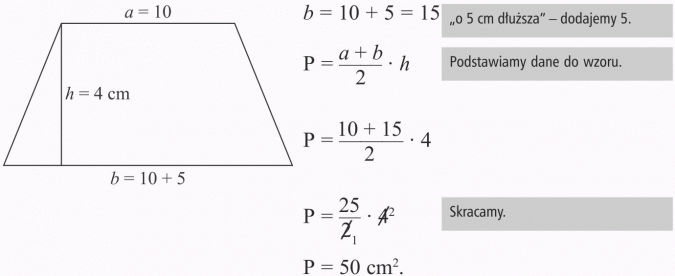
Oblicz pole trapezu, w którym wysokość ma długość 4 cm, jedna z podstaw ma długość 10 cm, a druga jest o 5 cm od niej dłuższa.

Pola figur. O 5 cm dłuższa - dodajemy 5. Podstawiamy dane do wzoru. Skracamy.

Odpowiedź:

Pole trapezu wynosi 50 cm².

Zadanie 20

Suma długości podstaw trapezu wynosi 7 cm, a wysokość ma 4 cm. Jakie jest pole tego trapezu?

Pola figur. Suma podstaw, więc za a + b podstawiamy 7.

Odpowiedź:

Pole trapezu wynosi 14 cm².

Zadanie 21

Obwód trapezu równoramiennego wynosi 28 cm, każde ramię ma długość 5 cm, a wysokość ma długość 4 cm. Oblicz pole tego trapezu.

Pola figur. Suma podstaw. Podstawiamy dane do wzoru. Zmieniamy strony. Aby obliczyć pole trapezu, musimy znać: sumę podstaw i wysokość. Za a + b wstawiamy 18. Skracamy.

Odpowiedź:

Pole trapezu wynosi 36 cm².

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Pola figur (na poziomie ucznia klasy 6)