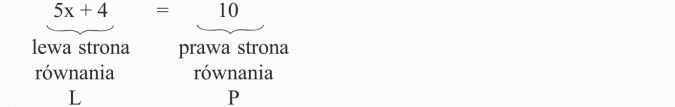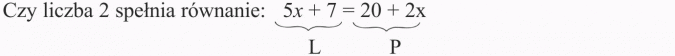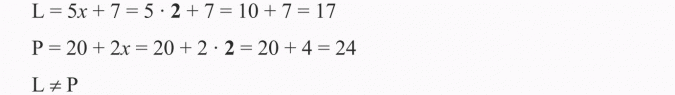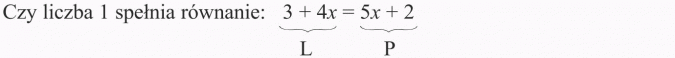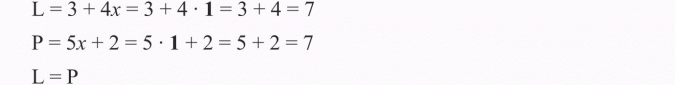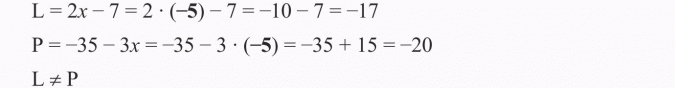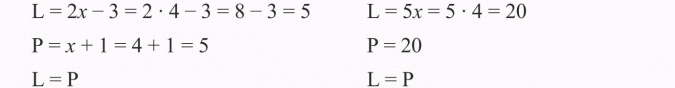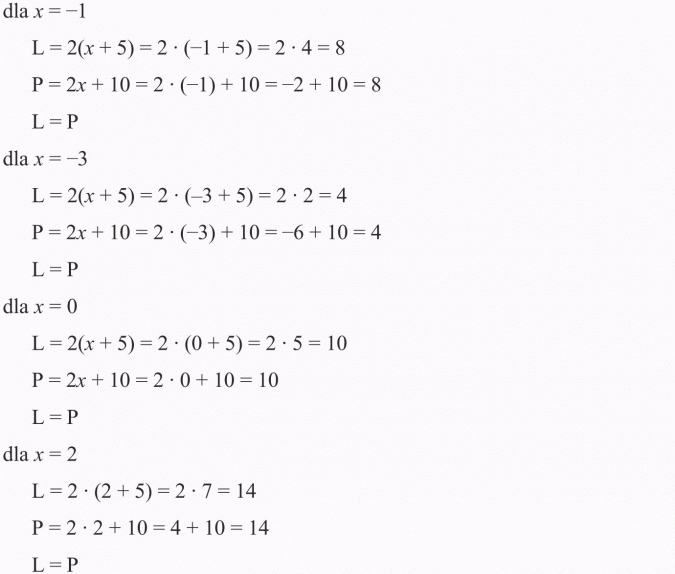Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Równanie
Liczbę spełniającą równanie nazywamy rozwiązaniem równania lub pierwiastkiem równania.
Liczba spełnia równanie, jeżeli po podstawieniu w miejsce niewiadomej czyni z tego równania zdanie prawdziwe (tzn. lewa strona równania równa się prawej).
Jak sprawdzić, czy liczba jest rozwiązaniem równania?
Przykład 1
Rozwiązanie:
Obliczamy wartość lewej i prawej strony równania, podstawiając w miejsce x liczbę 2, a następnie porównujemy otrzymane wyniki:
Odp.: Liczba 2 nie spełnia równania.
Przykład 2
Rozwiązanie:
Postępujemy podobnie jak w poprzednim przykładzie:
Odp.: Liczba 1 spełnia równanie.
Przykład 3
Sprawdź, czy liczba -5 jest rozwiązaniem równania 2x - 7 = -35 - 3x
Rozwiązanie:
Odp.: Liczba -5 nie jest rozwiązaniem równania.
Przykład 4
Sprawdź, czy liczba 4 jest rozwiązaniem równań:
Rozwiązanie:
Odp.: Liczba 4 jest rozwiązaniem obu równań.
Jeżeli dwa równania mają takie samo rozwiązanie, to równania te nazywamy równoważnymi.
Przykład 5
Sprawdź, czy liczby -1, -3, 0, 2 są rozwiązaniami równania: 2(x + 5) = 2x + 10
Rozwiązanie:
Podstawiamy kolejno do obu stron równania za x liczby:
-1, -3, 0, 2 i sprawdzamy czy lewa strona równa się prawej, a zatem:
Można jeszcze podstawić inne liczby (spróbuj) i okaże się, że każda z nich jest rozwiązaniem tego równania.
Zapamiętaj!
Równanie, którego rozwiązaniem jest każda liczba rzeczywista nazywamy równaniem tożsamościowym lub tożsamością.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.