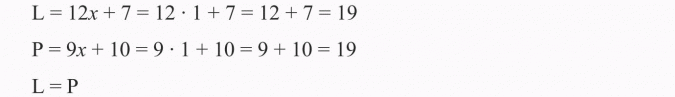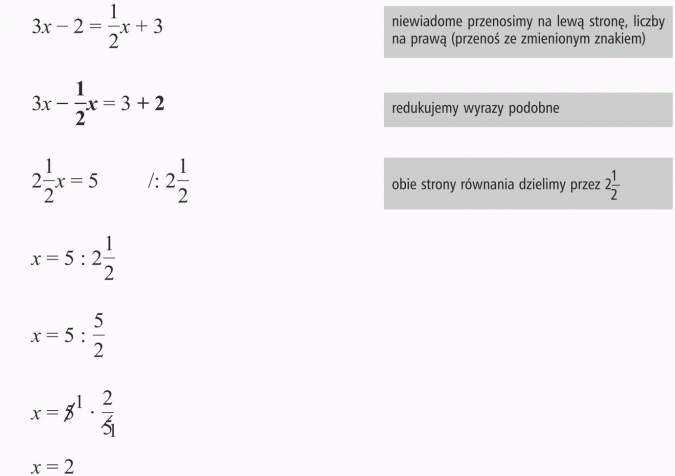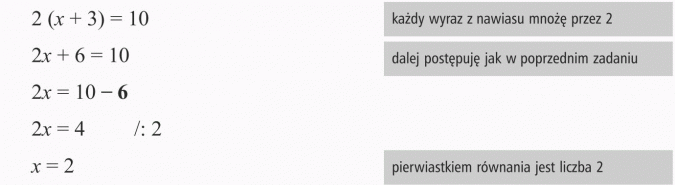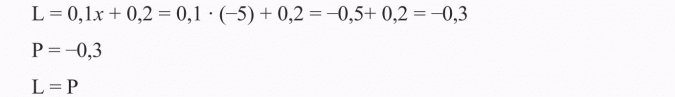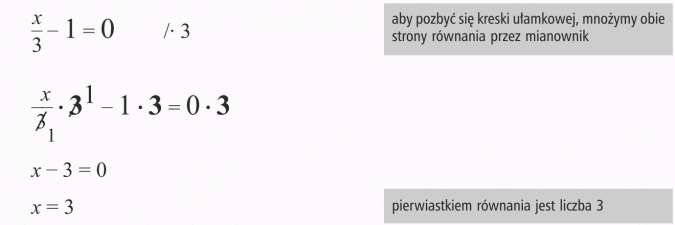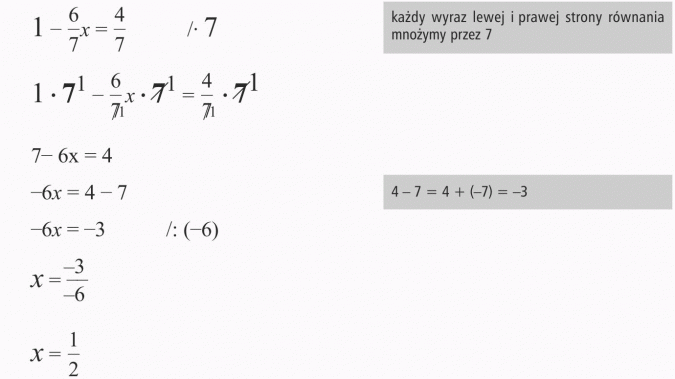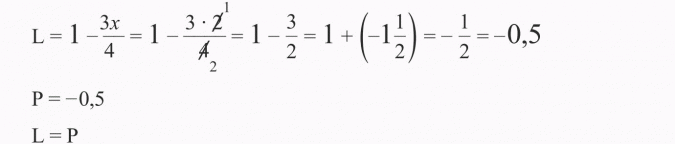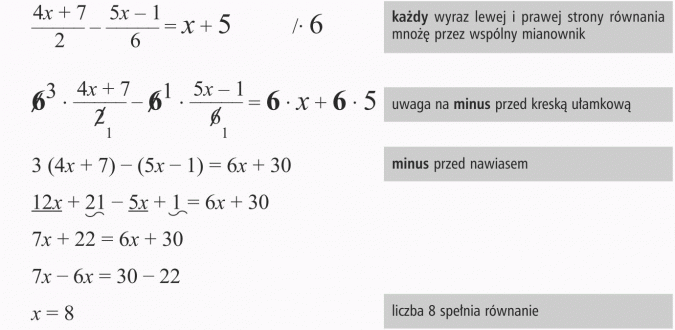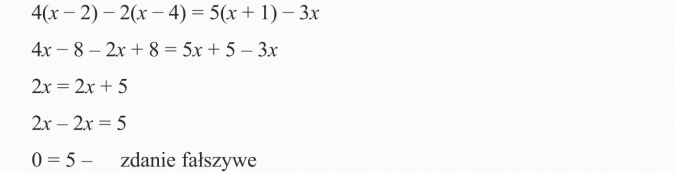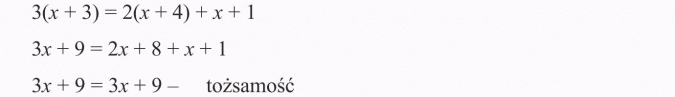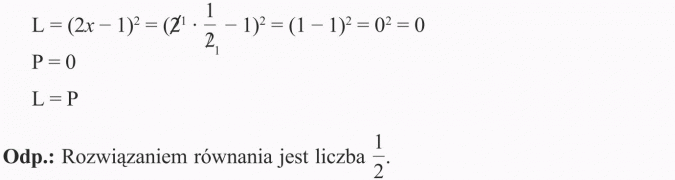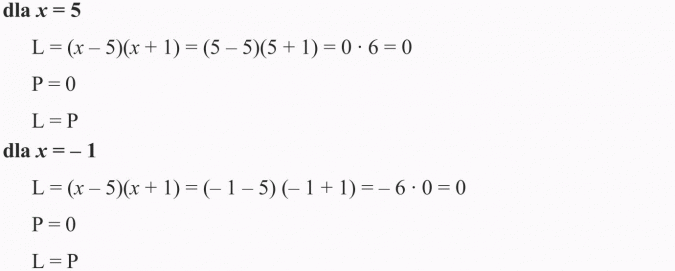Rozwiązywanie równań

Rozwiązać równanie to znaczy znaleźć wszystkie jego pierwiastki (liczby, które je spełniają) lub uzasadnić, że ich nie ma.

Reguły postępowania przy rozwiązywaniu równań:

1) Do obu stron równania można dodać takie samo wyrażenie.

2) Od obu stron równania można odjąć takie samo wyrażenie.

3) Obie strony równania można pomnożyć przez taką samą liczbę różną od zera.

4) Obie strony równania można podzielić przez taką samą liczbę różną od zera.

Rozwiązując równanie dążymy do tego, aby po jednej stronie równania znalazły się tylko niewiadome, a po drugiej tylko liczby.

Przykład 1

Rozwiąż równanie:

Rozwiązywanie równań. Staramy się otrzymać równanie, w którym po jednej stronie są niewiadome, a po drugiej stronie liczby. W tym celu do obu stron równania dodaję 10. Redukuję wyrazy podobne. Obie strony równania dzielę przez 2. Rozwiązaniem równania jest liczba 11.

Sprawdzam, czy liczba 11 spełnia równanie:

Odp.: Rozwiązaniem równania jest liczba 11.

Przykład 2

Rozwiązywanie równań. Od obu stron równania odejmuję liczbę 2. Redukuję wyrazy podobne. Obie strony równania dzielę przez (-1).

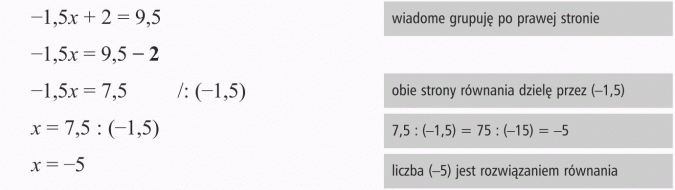
Odp.: Pierwiastkiem równania jest liczba - 6.

Przykład 3

Rozwiązywanie równań. Od obu stron równania odejmuję 9x. Redukuję wyrazy podobne. Od obu stron równania odejmuję 7. Obie strony równania dzielę przez 3.

Sprawdzenie:

Odp.: Rozwiązaniem równania jest liczba 1.

Uwaga

Nie zawsze dokonujemy sprawdzenia równania, czasem jest to bardziej pracochłonne niż samo rozwiązanie równania.

Zwróć uwagę, że jeśli w równaniu

12x + 7 = 9x + 10

przeniesiemy (zmieniając znak na przeciwny) wyrażenie 9x na lewą stronę, a liczbę 7 na prawą stronę, to otrzymamy równanie:

12x - 9x = 10 - 7

więc

3x = 3

Takie samo równanie otrzymaliśmy, odejmując od obu stron równania 9x oraz liczbę 7.

Przy rozwiązywaniu równań wygodnie jest przenosić (pamiętając o zmianie znaku na przeciwny) niewiadome na jedną stronę równania, a wiadome na drugą stronę równania.

Rozwiąż równania:

Zadanie 1

Rozwiązywanie równań. Niewiadome przenosimy na lewą stronę równania, a liczby na prawą; pamiętamy, że przenosząc zmieniamy znak na przeciwny. Redukujemy wyrazy podobne. Obie strony równania dzielimy przez 5 (dzielimy zawsze przez liczbę stojącą przed niewiadomą). Liczba 3 3/5 jest rozwiązaniem równania.

Zadanie 2

Rozwiązywanie równań. Niewiadome przenosimy na lewą stronę, liczby na prawą (przenoś ze zmienionym znakiem). Redukujemy wyrazy podobne. Obie strony równania dzielimy przez 2 1/2.

Odp.: Liczba 2 jest pierwiastkiem równania.

Zadanie 3

Rozwiązywanie równań. Opuszczam nawias, uwaga na minus przed nawiasem. Redukuję wyrazy podobne. Liczbę 1 przenoszę ze zmienionym znakiem na prawą stronę równania. Obie strony równania dzielę przez 5.

Odp.: Rozwiązaniem równania jest liczba 1.

Zadanie 4

Rozwiązywanie równań. Wiadome grupuję po prawej stronie. Obie strony równania dzielę przez (-1,5). Liczba (-5) jest rozwiązaniem równania.

Zadanie 5

Rozwiązywanie równań. Każdy wyraz z nawiasu mnożę przez 2. Dalej postępuję jak w poprzednim zadaniu. Pierwiastkiem równania jest liczba 2.

Zadanie 6

Rozwiązywanie równań. Opuszczam nawias. Redukuję wyrazy podobne. Rozwiązaniem równania jest liczba 4.

Zadanie 7

Rozwiązywanie równań. Opuszczam nawias. Redukuję wyrazy podobne. Liczbę (-17) przenoszę na prawą stronę ze zmienionym znakiem. Liczba (-4) jest pierwiastkiem równania.

Zadanie 8

Rozwiązywanie równań. Opuszczam nawiasy, dalej postępuję jak w zadaniu poprzednim. Rozwiązaniem równania jest liczba (-9).

Zadanie 9

Rozwiązywanie równań. Redukuję wyrazy podobne po obu stronach równania.

Zadanie 10

Rozwiązywanie równań. Opuszczam nawiasy. Niewiadome przenoszę na lewą stronę, a liczby na prawą; przy przenoszeniu zmieniam znaki na przeciwne.

Zadanie 11

Rozwiązywanie równań. Wygodnie jest obie strony równania pomnożyć przez 10 (pozbywamy się w ten sposób ułamków dziesiętnych), pamiętaj, żeby każdy wyraz pomnożyć przez 10. Rozwiązaniem równania jest liczba -5.

Sprawdźmy:

Zadanie 12

Rozwiązywanie równań. Obie strony równania mnożę przez 10. Niewiadome przenoszę na lewą stronę, a liczby na prawą, pamiętając o zmianie znaku na przeciwny.

Zadanie 13

Rozwiązywanie równań. Każdy wyraz lewej i prawej strony równania mnożę przez 10. Opuszczam nawias, redukuję wyrazy podobne.

Wyjaśnię teraz jak radzić sobie z równaniami zawierającymi wyrażenia ułamkowe.

Zadanie 14

Rozwiązywanie równań. Aby pozbyć się kreski ułamkowej, mnożymy obie strony równania przez mianownik. Pierwiastkiem równania jest liczba 3.

Zadanie 15

Rozwiązywanie równań. Obie strony równania mnożę przez 5. Przed mnożeniem skracam. Rozwiązaniem równania jest liczba -1 1/2.

Zadanie 16

Rozwiązywanie równań. Każdy wyraz lewej i prawej strony równania mnożymy przez 7.

Sprawdźmy:

Rozwiązywanie równań. Rozwiązaniem równania jest liczba 1/2.

Zadanie 17

Rozwiązywanie równań. Tutaj można nawias pomnożyć przez 1/6, ale łatwiej będzie, jeżeli obie strony równania pomnożymy przez 6 (unikniemy działań na ułamkach). Opuszczamy nawias. Liczba 7 jest rozwiązaniem równania.

Zadanie 18

Rozwiązywanie równań. Postępujemy podobnie jak w zadaniu poprzednim. Liczba 8 jest pierwiastkiem równania.

Zadanie 19

Rozwiązywanie równań. Obie strony równania mnożę przez 3, aby pozbyć się kreski ułamkowej. Obie strony równania dzielimy przez 11. Zamieniamy równanie stronami, bo tak lepiej wygląda.

Zadanie 20

Rozwiązywanie równań. Uwaga na minus przed kreską ułamkową. Usuwamy nawias, zmieniając znaki w nawiasie na przeciwne. Pierwiastkiem równania jest liczba 1.

Zadanie 21

Rozwiązywanie równań. Obie strony równania mnożę przez 2. Uwaga! minus przed kreską ułamkową. Uważaj, minus przed nawiasem. Zmień znak, przenosząc wyrażenia na drugą stronę równania. Liczba -2 2/3 jest rozwiązaniem równania.

Zadanie 22

Rozwiązywanie równań. Teraz wygodnie jest obie strony równania pomnożyć przez wspólny mianownik, czyli przez 12. Rozwiązaniem równania jest liczba 7 1/5.

Zadanie 23

Rozwiązywanie równań. Obie strony równania mnożę przez wspólny mianownik, czyli przez 4. Liczba -3 jest rozwiązaniem równania.

Zadanie 24

Rozwiązywanie równań. Każdy wyraz lewej i prawej strony równania mnożę przez 4.

Sprawdzenie:

Odp.: Rozwiązaniem równania jest liczba 2.

Zadanie 25

Rozwiązywanie równań. Obie strony równania mnożę przez wspólny mianownik, czyli 6. Otrzymuję prostsze równanie, które rozwiązuję podobnie jak poprzednie.

Sprawdzenie:

Odp.: Rozwiązaniem równania jest liczba (- 1).

Zadanie 26

Rozwiązywanie równań. W celu pozbycia się kresek ułamkowych mnożę obie strony równania przez wspólny mianownik, tzn. przez 15. Usuwam nawiasy. Liczba 1/26 jest pierwiastkiem równania.

Zadanie 27

Rozwiązywanie równań. Opuszczam nawiasy w licznikach, mnożąc każdy wyraz I nawiasu przez 5, a II przez 3. Obie strony równania mnożę przez wspólny mianownik. Opuszczam nawiasy. Redukuję wyrazy podobne po lewej stronie równania. Pierwiastkiem równania jest liczba 1.

Zadanie 28

Rozwiązywanie równań. Każdy wyraz lewej i prawej strony równania mnożę przez wspólny mianownik. Uwaga na minus przed kreską ułamkową. Minus przed nawiasem. Liczba 8 spełnia równanie.

Zadanie 29

Rozwiązywanie równań. Najpierw usuwam nawias okrągły (uwaga! minus przed nawiasem). Teraz opuszczam nawias kwadratowy. Redukuję wyrazy podobne. Liczba 3 spełnia równanie.

Wszystkie równania, które rozwiązywaliśmy dotąd, miały tylko jeden pierwiastek (jedna liczba je spełniała).

Nie zawsze tak jest.

Zadanie 30

5 (x - 8) = 5x + 6

5x - 40 = 5x + 6

5x - 5x = 6 + 40

0 = 46 - zdanie fałszywe

Równanie nie ma rozwiązania.

Takie równanie nazywamy sprzecznym.

Inne przykłady równań sprzecznych:

Zadanie 31

Rozwiązywanie równań. Usuwamy nawiasy. Zdanie prawdziwe.

To równanie spełnia każda liczba rzeczywista (sprawdź).

Równania takie nazywamy równaniem tożsamościowymi lub tożsamością.

Zadanie 32

Odp.: Równanie nie ma rozwiązania, jest to równanie sprzeczne.

Zadanie 33

Odp.: To równanie spełnia każda liczba rzeczywista, jest to równanie tożsamościowe.

Sprawdźmy:

Rozwiązywanie równań. Dla x = 0. Dla x = 1.

PROBLEM

Rozwiąż równania:

Zadanie 34

Rozwiązywanie równań. Potęgę zapisujemy w postaci iloczynu jednakowych czynników, bo a^2 = a x a, więc... Iloczyn jest równy 0 wtedy i tylko wtedy, gdy jeden z czynników jest równy 0, ponieważ są to jednakowe czynniki, to wystarczy jeden z nich przyrównać do zera i rozwiązać równanie.

Sprawdzenie

Zadanie 35

Rozwiązywanie równań. Postępujemy podobnie jak w zadaniu 1, iloczyn jest równy 0, gdy jeden z jego czynników równa się 0. Rozwiązujemy każde z równań. Okazuje się, że rozwiązaniem równania są dwie liczby.

Sprawdzenie:

Rozwiązywanie równań. Dla x = 0, dla x = 2.

Odp.: Równanie spełniają dwie liczby: 0 i 2.

Zadanie 36

Rozwiązywanie równań. Rozwiązujemy podobnie do zadania 1 i 2. Każdy z czynników iloczynu przyrównujemy do zera, a następnie rozwiązujemy otrzymane równania. Równanie ma dwa pierwiastki.

Sprawdzenie:

Rozwiązywanie równań. Dla x = 5. Dla x = -1.

Odp.: Rozwiązaniem równania są dwie liczby: 5 i (-1).

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Rozwiązywanie równań