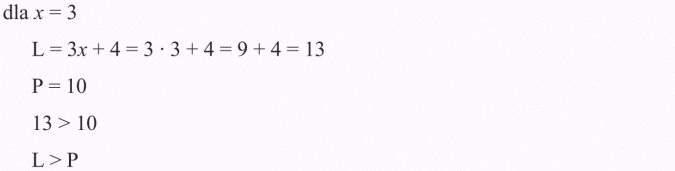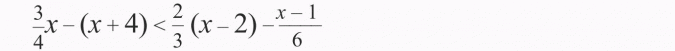Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
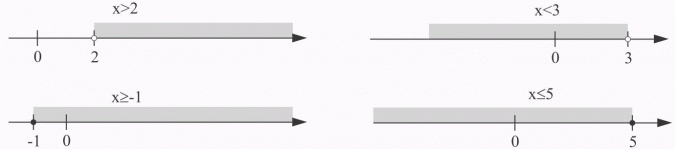
Zbiór rozwiązań nierówności przedstawiamy na osi liczbowej:
Zwróć uwagę na kółeczka na osi liczbowej:
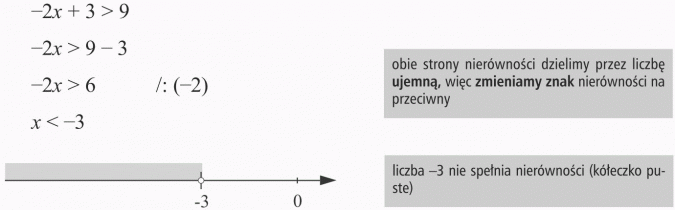
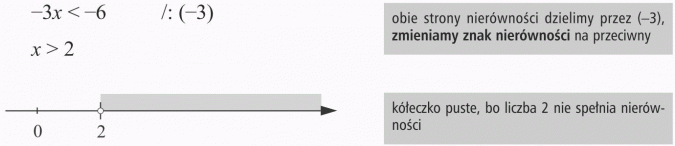
- puste w środku przy nierówności ostrej oznacza, że końcowy punkt nie należy do rozwiązania,
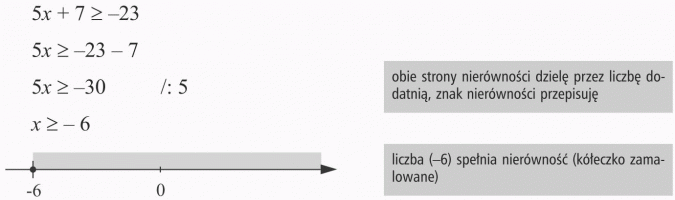
- zamalowane przy nierówności nieostrej (słabej) oznacza, że końcowy punkt należy do rozwiązania nierówności.
Przy rozwiązywaniu nierówności postępujemy podobnie jak przy rozwiązywaniu równań (patrz reguły postępowania) z jednym wyjątkiem, a mianowicie:
Jeżeli mnożymy lub dzielimy obie strony nierówności przez liczbę ujemną zmieniamy znak nierówności na przeciwny.
Rozwiąż nierówności i zaznacz ich zbiory rozwiązań na osi liczbowej:
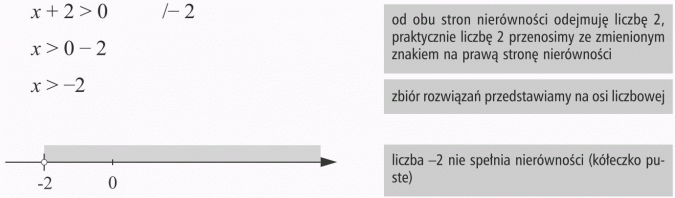
Odp.: Rozwiązaniem nierówności są wszystkie liczby większe od (-2).
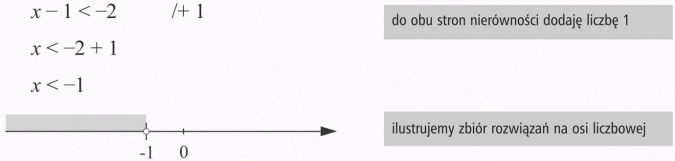
Odp.: Rozwiązaniem nierówności są wszystkie liczby mniejsze od (-1).
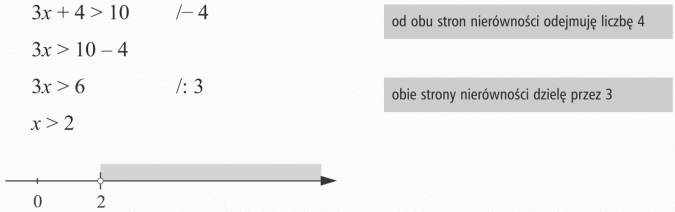
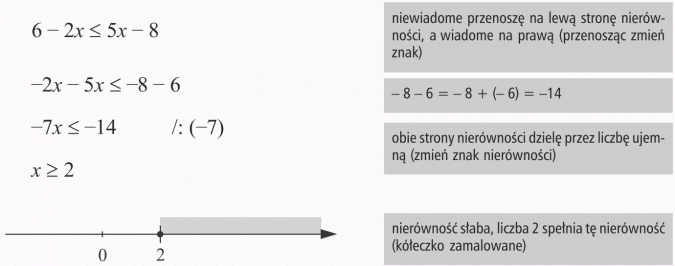
Odp.: Rozwiązaniem nierówności są wszystkie liczby większe od 2.
Sprawdźmy:
Podstawmy za x liczbę np. 3:
Odp.: Wszystkie liczby rzeczywiste mniejsze od (-3) spełniają nierówność.
Odp.: Rozwiązaniem nierówności są wszystkie liczby większe od 2.
Odp.: Nierówność spełniają wszystkie liczby większe od -6 oraz liczba -6.
Odp.: Rozwiązaniem nierówności są wszystkie liczby większe od 2 i liczba 2.
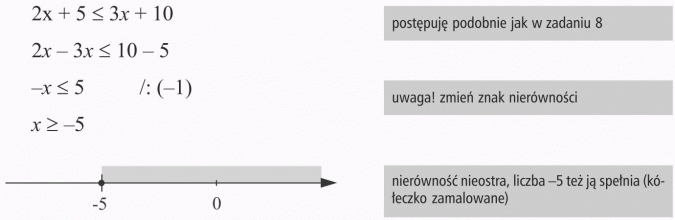
Odp.: Rozwiązaniem nierówności jest liczba -5 oraz liczby większe od -5.
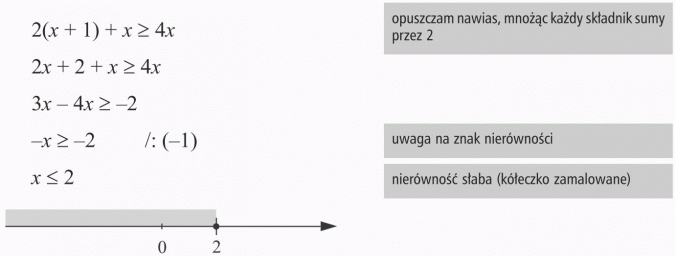
Odp.: Nierówność spełniają wszystkie liczby mniejsze lub równe 2.
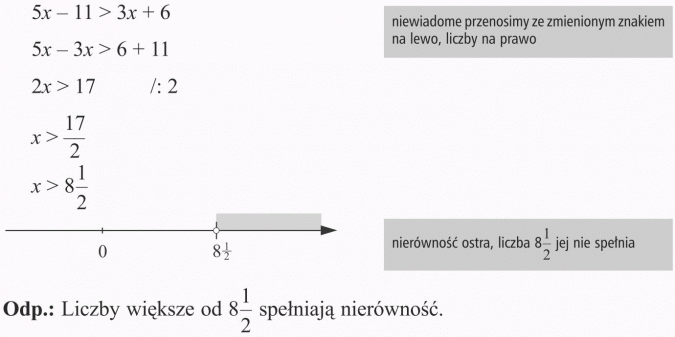
Odp.: Rozwiązaniem nierówności jest każda liczba większa od 7.
Odp.: Nierówność spełnia każda liczba większa od 2.
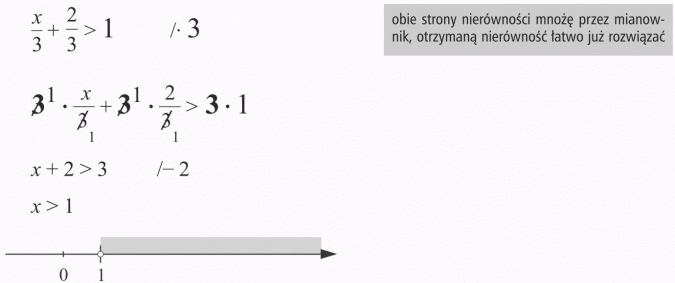
Odp.: Wszystkie liczby większe od 1 spełniają nierówność.
Odp.: Każda liczba rzeczywista mniejsza lub równa 5 spełnia nierówność.
Podaj wszystkie liczby naturalne spełniające nierówność:
Rozwiązanie:
Najpierw rozwiązujemy nierówność podobnie jak poprzednio:
Odp.: Liczby naturalne, które spełniają nierówność to: 0, 1, 2.
Znajdź najmniejszą liczbę naturalną, która spełnia nierówność:
Rozwiązanie:
Odp.: Ta liczba to 1.
Podaj największą liczbę całkowitą nie spełniającą tej nierówności:
Rozwiązanie:
Rozwiążmy nierówność:
Przypomnienie: liczby całkowite to: ... -3, -2, -1, 0, 1, 2, 3,...
Z ilustracji graficznej widać, że największa liczba całkowita, która nie spełnia tej nierówności to 10.
Odp.: Ta liczba to 10.
Podaj najmniejszą liczbę całkowitą, która jest rozwiązaniem nierówności:
Rozwiązanie:
Z rozwiązania przedstawionego na osi liczbowej odszukujemy najmniejszą liczbę całkowitą, która spełnia nierówność.
Nietrudno zauważyć, że ta liczba to (-3).
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.