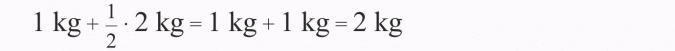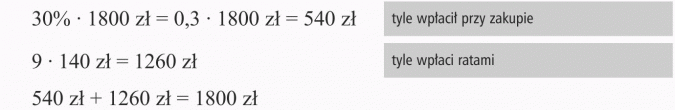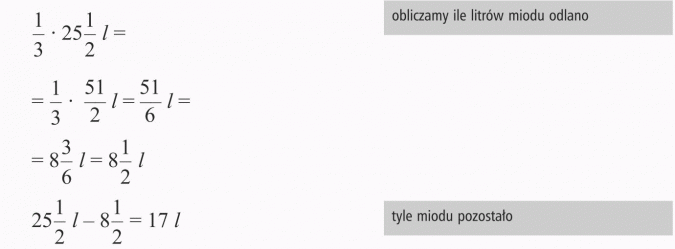Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Zadania tekstowe większości uczniom sprawiają duże problemy. Mam nadzieję, że jednak uda mi się zainteresować Cię nimi.
W tym rozdziale znajdziesz 24 bardzo dokładnie wyjaśnione i rozwiązane zadania o różnym stopniu trudności.
Rozwiązując zadania tekstowe, czytaj zawsze bardzo uważnie, kilka razy treść zadania.
Zadania staraj się rozwiązywać według następującego schematu:
1. Analiza zadania: małą literą alfabetu ustalamy niewiadomą oraz układamy wyrażenia zgodnie z treścią zadania.
2. Ułożenie równania: wybieramy (z analizy zadania) takie dwa wyrażenia, które przedstawiają tę samą wielkość i łączymy je znakiem równości.
3. Rozwiązanie równania.
4. Sprawdzenie wyniku z treścią (z warunkami) zadania.
Uwaga! Ważne!
Sprawdzamy (czytając treść zadania ponownie), czy wynik spełnia warunki zadania. To nie to samo, co sprawdzenie równania, bo załóżmy, że równanie rozwiązaliśmy dobrze, ale mogliśmy popełnić błąd przy jego układaniu.
5. Podanie odpowiedzi.
Po rozwiązaniu zadania tekstowego jeszcze raz przeczytaj jego treść. Upewnij się, czy na pewno odpowiedziałeś na pytanie.
Rozwiązanie
Analiza zadania:
Ułożenie i rozwiązanie równania:
Odp.: Należy jeszcze dowieźć 65 kg soli.
Dawid jest 5 razy młodszy od mamy. Suma lat Dawida i mamy wynosi 48 lat. Ile lat ma Dawid?
Rozwiązanie:
Analiza zadania:
Ułożenie i rozwiązanie równania:
Sprawdzenie z treścią:
Odp.: Dawid ma 8 lat.
Rozwiązanie:
Sprawdzam z treścią:
Odp.: Klasa liczy 18 uczniów.
Rozwiązanie:
Sprawdzenie z treścią:
Odp.: Duży arbuz waży 9 kg.
Pitagoras zapytany, ilu ma uczniów odpowiedział: połowa studiuje matematykę, czwarta część fizykę, siódma część uczy się milczenia, ponadto mam jeszcze trzech uczniów. Ilu uczniów miał Pitagoras?
Rozwiązanie:
Sprawdzenie z treścią:
Sprawdzam (czytając treść zadania) czy liczba 28 spełnia warunki zadania
Zgadza się!
Odp.: Pitagoras miał 28 uczniów.
Suma trzech liczb wynosi 44. Znajdź te liczby, jeżeli wiadomo, że druga jest 3 razy większa od pierwszej, a trzecia jest o 2 większa od drugiej
Rozwiązanie:
Sprawdzenie z treścią:
Sprawdzam, czy suma obliczonych liczb wynosi 44.
6 + 18 + 20 = 44 TAK
Odp.: Te liczby to 6, 18 i 20.
Cegła waży kilo i pół cegły. Ile waży cegła?
Rozwiązanie:
Sprawdzenie z treścią:
Odp.: Cegła waży 2 kg.
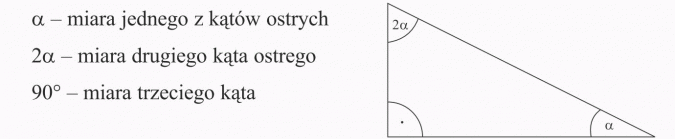
W trójkącie prostokątnym jeden z kątów ostrych jest dwa razy większy od drugiego. Oblicz miary tych kątów.
Rozwiązanie:
Pamiętaj!
Suma kątów wewnętrznych każdego trójkąta wynosi 180°.
Sprawdzenie z treścią:
30° + 60° + 90° = 180°
Odp.: Miary kątów ostrych trójkąta wynoszą 30° i 60°.
Działka ma kształt prostokąta, którego dłuższy bok ma o 15 m więcej niż krótszy, a obwód ma 70 m.
Znajdź boki tej działki.
Rozwiązanie:
Sprawdzenie z treścią:
2 · 10 m + 2 · 25 m = 20 m + 50 m = 70 m
Odp.: Boki działki mają długość 10 m i 25 m.
Średnia zarobków Wojtka za ostatni kwartał wyniosła 1800 zł. Ile Wojtek zarobił w grudniu, jeśli w październiku zarobił 1630 zł, a w listopadzie 2120 zł.
Rozwiazanie:
Średnią zarobków oblicza się podobnie jak liczysz średnią ocen, tzn. dodajesz wartości ocen (wartość piątki to 5, wartość czwórki to 4 itd.) i dzielisz przez liczbę ocen.
Przy obliczaniu średnich zarobków w IV kwartale sumujesz zarobki z października, listopada i grudnia i dzielisz przez 3 (liczbę miesięcy).
Sprawdzenie z treścią:
Odp.: W grudniu Wojtek zarobił 1650 zł.
Rozwiązanie:
Sprawdzenie z treścią:
Suma wieku Ani, Pauliny i Staszka wynosi 52 lata. Staszek jest dwa razy starszy od Ani, a Paulina o 4 lata starsza od Ani. Ile lat ma Staszek?
Rozwiązanie:
Sprawdzenie z treścią:
12 + 4 = 16 - wiek Pauliny
12 + 16 + 24 = 52 - suma wieku Ani, Staszka i Pauliny
Odp.: Staszek ma 24 lata.
Kamila ma 14 lat, a Ela jest o 2 lata starsza. Za ile lat będą miały razem 40 lat?
Rozwiązanie:
x - za tyle lat będą miały razem 40 lat
Przedstawmy analizę zadania w tabelce:
| wiek obecnie | wiek za x lat | |
|---|---|---|
| Kamila | 14 | 14 + x |
| Ela | 14 + 2 = 16 | 16 + x |
Sprawdzenie z treścią:
Odp.: Za 5 lat będą mieć razem 40 lat.
Ojciec ma 45 lat, a synowie 10 i 8 lat. Po ilu latach ojciec będzie miał tyle lat, co obaj synowie razem?
Rozwiązanie:
x - po tylu latach ojciec będzie miał tyle lat, co obaj synowie razem
| wiek obecnie | wiek po x latach | |
|---|---|---|
| ojciec | 45 | 45 + x |
| starszy syn | 10 | 10 + x |
| młodszy syn | 8 | 8 + x |
Sprawdzenie z treścią:
45 + 27 = 72 - wiek ojca za 27 lat
10 + 27 = 37 - wiek starszego syna za 27 lat
8 + 27 = 35 - wiek młodszego syna za 27 lat
37 + 35 = 72 - suma lat obu synów za 27 lat (wynosi tyle co wiek ojca)
Odp.: Po 27 latach ojciec będzie miał tyle lat co obaj synowie razem.
W pewnej liczbie dwucyfrowej cyfra jedności jest o 2 większa od cyfry dziesiątek. Jeżeli od tej liczby odejmiemy potrojoną cyfrę dziesiątek, to otrzymamy 34. Znajdź tę liczbę.
Rozwiązanie:
Przypomnienie:
Liczbę dwucyfrową zapisujemy:
10 a + b, gdzie
a - cyfra dziesiątek
b - cyfra jedności
U nas w zadaniu oznaczamy:
a zatem ta liczba to 46
Odp.: Ta liczba to 46.
Turysta w ciągu 3 dni przejechał 684 km. Pierwszego dnia przejechał 2 razy więcej niż drugiego, a trzeciego o 20% mniej niż drugiego. Ile km przejechał trzeciego dnia?
Rozwiązanie:
Sprawdzenie z treścią:
Odp.: Turysta trzeciego dnia przejechał 144 km.
Przy zakupie komputera Staszek wpłacił 30% jego wartości. Pozostałą część należności sprzedawca rozłożył na 9 rat po 140 zł każda. Ile kosztował komputer?
Rozwiązanie:
Sprawdzenie z treścią:
Odp.: Komputer kosztował 1800 zł.
Państwo Gemrowie (rodzice i troje dzieci) spędzili 14 dni na wczasach w Bieszczadach. Opłata za dziecko wynosiła 50% opłaty za osobę dorosłą. Za pobyt zapłacili łącznie 2940 zł. Ile wynosiła opłata za 1 dzień pobytu dziecka?
Rozwiązanie:
Sprawdzenie z treścią:
Odp.: Za jeden dzień pobytu dziecka zapłacono 30 zł.
Ania i Staszek zbierali grzyby. Staszek uzbierał 3 razy więcej niż Ania. Gdyby oddał Ani 15 grzybów, to oboje mieliby tyle samo.
Ile grzybów ma Ania, a ile Staszek?
Rozwiązanie:
Sprawdzenie z treścią:
Odp.: Ania ma 15 grzybów, a Staszek 45.
Za bilety wstępu na wystawę grupa turystów zapłaciła 650 zł. Dorośli płacili po 25 zł, a dzieci po 15 zł za bilet. Ilu dorosłych, a ile dzieci było w tej grupie, jeżeli dorosłych było o 10 więcej niż dzieci.
Rozwiązanie:
Sprawdzenie z treścią zadania:
Odp.: W grupie było 10 dzieci i 20 osób dorosłych.
Cena książki po obniżce o 30%, a następnie o 15% wynosi 11,90 zł. Oblicz cenę początkową.
Rozwiązanie:
Sprawdzenie z treścią:
Odp.: Cena początkowa książki wynosiła 20 zł.
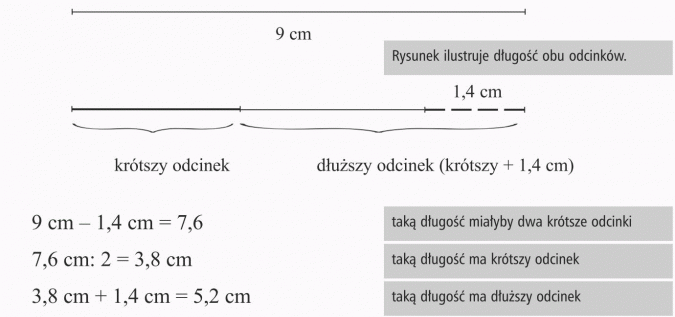
Dwa odcinki mają łącznie 9 cm długości. Jeden z nich jest o 1,4 cm dłuższy od drugiego. Jaka jest długość każdego z nich?
Rozwiązanie:
Nie zawsze każde zadanie trzeba rozwiązywać za pomocą równania.
Czasem do rozwiązania warto wykorzystać rysunek.
Sprawdzenie z warunkami zadania:
Odp.: Odcinki mają długość 3,8 cm oraz 5,2 cm.
Rozwiązanie:
Odp.: W słoiku pozostało 17 l miodu.
Zmieszano dwa rodzaje cukierków: 2 kg po 23 zł za 1 kg i 3 kg po 24 zł za 1 kg. Jaka powinna być cena 1 kg mieszanki?
Rozwiązanie:
Odp.: 1 kg mieszanki powinien kosztować 23,60 zł.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
![Zadania tekstowe. Waga arbuza [kg]. Te dwa wyrażenia oznaczają to samo, łączymy je znakiem równości.](https://staticopracowania.iplsc.com/opracowania_prod_static/images/189040/zadania_tekstowe_11.gif)
![Zadania tekstowe. Waga cegły [kg]. To wynika z treści zadania.](https://staticopracowania.iplsc.com/opracowania_prod_static/images/189043/zadania_tekstowe_16.gif)
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.