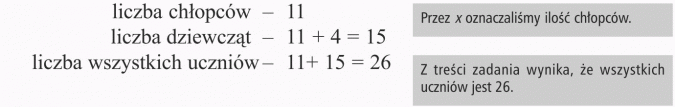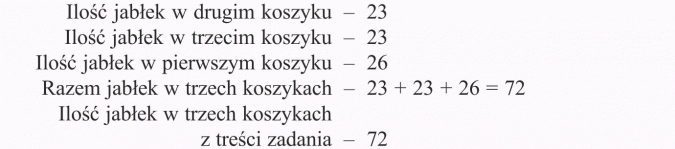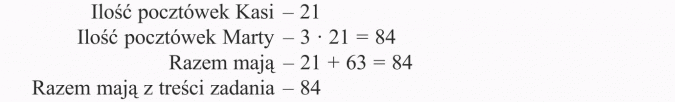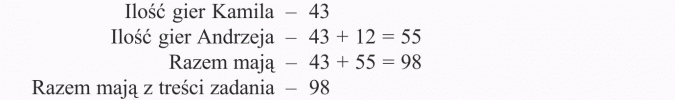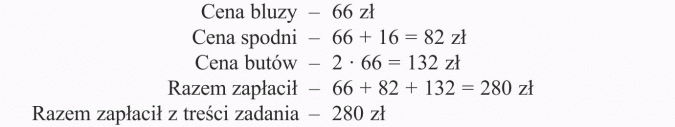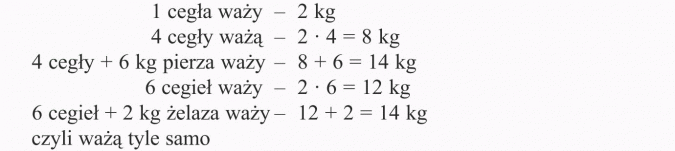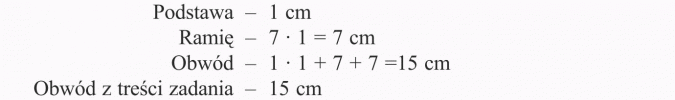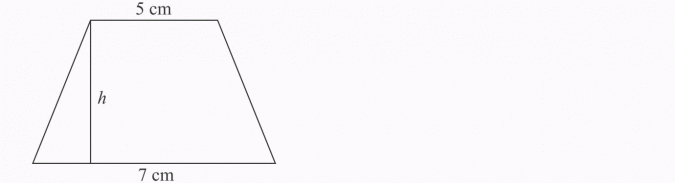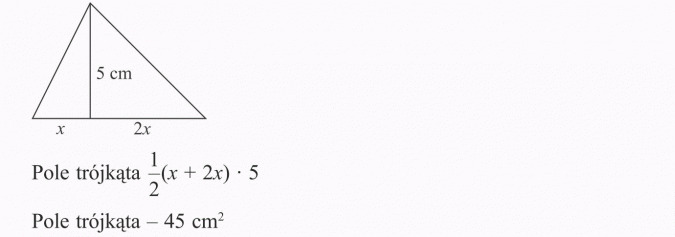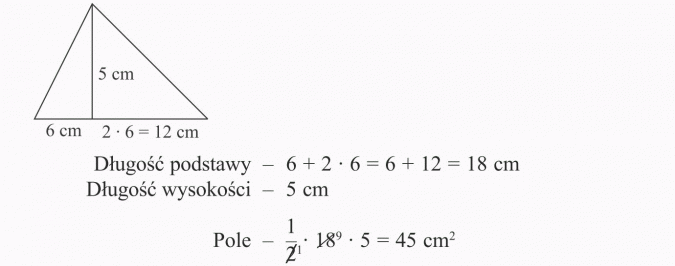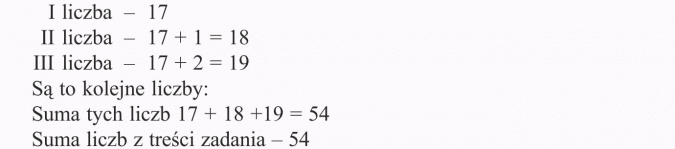Rozwiązywanie zadań tekstowych

Zadanie 1

W klasie VI d uczy się 26 uczniów. Dziewcząt jest o 4 więcej niż chłopców. Ilu chłopców i ile dziewcząt jest w tej klasie?

I etap - ustalamy niewiadomą, oznaczamy ją literą:

Rozwiązywanie zadań tekstowych. Liczba chłopców, liczba dziewcząt. Bo jest ich o 4 więcej.

II etap - zapisujemy równanie

Rozwiązywanie zadań tekstowych. Liczba chłopców, liczba dziewcząt, liczba wszystkich uczniów.

III etap - rozwiązujemy równanie

Rozwiązywanie zadań tekstowych. Redukujemy wyrazy podobne po lewej stronie. Przenosimy 4 na prawą stronę - zmieniamy znak. Dzielimy obie strony przez liczby stojące przy x.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Liczba chłopców, liczba dziewcząt, liczba wszystkich uczniów. Przez x oznaczaliśmy ilość chłopców. Z treści zadania wynika, że wszystkich uczniów jest 26.

V etap - zapisujemy odpowiedź:

Odpowiedź:

W klasie jest 11 chłopców i 15 dziewcząt.

Zadanie 2

Metalowy pręt o długości 8,4 m rozcięto na dwie części, z których jedna jest 2 razy dłuższa od drugiej. Jaką długość mają te części?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Długość krótszej części, długość dłuższej części. 2 razy dłuższa sugeruje mnożenie przez 2.

II etap - zapisujemy równanie:

Rozwiązywanie zadań tekstowych. Bo długość pręta wynosi 8,4 m.

III etap - rozwiązujemy równania:

Rozwiązywanie zadań tekstowych. Redukujemy wyrazy podobne po lewej stronie. Dzielimy przez 3, bo stoi przy x.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Długość krótszej części, długość dłuższej części, długość pręta (krótsza część + dłuższa część), długość pręta z warunków zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Jedna część ma 2,8 m, a druga 5,6 m.

Zadanie 3

Za 6 długopisów po 1,50 zł każdy i 4 zeszyty Ala zapłaciła 18,80 zł. Ile kosztował zeszyt?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Cena zeszytu, tyle kosztowały 4 zeszyty, tyle kosztowały długopisy, tyle kosztowały wszystkie zakupy Ali. Ilość x cena = kwota do zapłaty.

II etap - zapisujemy równanie:

4x + 6 · 1,50 = 18,80

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Przenosimy 9 na prawą stronę - zmieniamy znak. Dzielimy obie strony przez 4.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią:

Rozwiązywanie zadań tekstowych. Cena zeszytu. Za 4 zeszyty zapłacono. Za długopisy zapłacono. Za zakupy zapłacono - z treści zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Zeszyt kosztował 2,45 zł.

Zadanie 4

W trzech koszykach jest razem 72 jabłek. W pierwszym jest 26 jabłek, a w dwóch pozostałych po tyle samo. Ile jabłek jest w każdym koszyku?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Ilość jabłek w drugim koszyku, ilość jabłek w trzecim koszyku, ilość jabłek w pierwszym koszyku, ilość jabłek w trzech koszykach. Bo w obu jest tyle samo.

II etap - zapisujemy równanie:

Rozwiązywanie zadań tekstowych. Razem w trzech koszykach jest x + x + 26, a z treści zadania wynika, że wszystkich jabłek jest 72.

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Przenosimy 26 na prawą stronę ze zmienionym znakiem. Dzielimy przez 2, bo dwa stoi przy x.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią:

Rozwiązywanie zadań tekstowych. Ilość jabłek w drugim koszyku, ilość jabłek w trzecim koszyku, ilość jabłek w pierwszym koszyku, razem jabłek w trzech koszykach, ilość jabłek w trzech koszykach - z treści zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

W koszykach jest następująca ilość jabłek: 23, 23, 26.

Zadanie 5

Marta ma 3 razy więcej pocztówek od Kasi. Razem mają 84 pocztówki. Ile pocztówek ma każda z dziewczynek?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Ilość pocztówek Kasi. Ilość pocztówek Marty. Ilość pocztówek, które mają razem. Tyle pocztówek mają razem - z treści zadania. 3 razy więcej - mnożymy przez 3.

II etap - zapisujemy równanie

x + 3x = 84

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Redukujemy liczby podobne po lewej stronie. Dzielimy przez 4, bo stoi obok x.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Ilość pocztówek Kasi, ilość pocztówek marty, razem mają z treści zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Kasia ma 21 pocztówek, a Marta 63 pocztówki.

Zadanie 6

Andrzej ma 12 gier komputerowych więcej niż Kamil. Razem mają 98 gier. Ile gier ma każdy z nich?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Ilość gier komputerowych Kamila, ilość gier Andrzeja, ilość gier, które mają razem - z treści zadania, o 12 więcej dodajemy.

II etap - zapisujemy równanie:

x + x + 12 = 98

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Redukujemy wyrazy podobne po lewej stronie. Przenosimy 12 na prawą stronę - zmieniamy znak.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Ilość gier Kamila, ilośc gier Andrzeja, razem mają z treści zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Kamil ma 43, a Andrzej 55 gier komputerowych.

Zadanie 7

W klasie 6a jest 26 uczniów. Chłopców jest dwa razy więcej niż dziewcząt. Ilu jest chłopców, a ile dziewcząt w tej klasie?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Ilość dziewcząt, ilość chłopców, ilość uczniów w klasie, ilość uczniów w klasie z warunków zadania.

II etap - zapisujemy równanie:

x + 2x = 26

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Redukcja wyrazów podobnych po lewej stronie. Wyciągamy całości.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Ilość dziewcząt.

Zadanie nie ma rozwiązania, gdyż ilość dziewcząt powinna być wyrażona w liczbach naturalnych, nie w ułamkach.

Zadanie 8

Pan Kowalski kupił sobie bluzę, spodnie i buty. Zapłacił razem 280 zł. Spodnie kosztowały o 16 zł więcej niż bluza, a buty dwa razy więcej niż bluza. Ile kosztowała bluza, ile spodnie, a ile buty?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Cena bluzy, cena spodni, cena butów, tyle kosztowaly zakupy z treści zadania.

II etap - zapisujemy równanie:

x + x + 16 + 2x = 280

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Redukujemy wyrazy podobne po lewej stronie. Przenosimy 16 na prawą stronę - zmieniamy znak.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Cena bluzy, cena spodni, cena butów, razem zapłacił z treści zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Bluza kosztowała 66 zł, spodnie 82 zł, a buty 132 zł.

Zadanie 9

Kwotę 850 zł wypłacono banknotami po 20 zł, 50 zł i 100 zł. Ile było banknotów każdej wartości, jeśli setek było dwa razy więcej niż pięćdziesiątek, a dwudziestek o 4 mniej niż pięćdziesiątek i setek razem?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Ilość banknotów pięćdziesięciozłotowych, ilość banknotów stuzłotowych (bo dwa razy więcej), ilość banknotów dwudziestozłotowych (bo o 4 mniej), to ktowa wypłacona banknotami 50 zł, to kwota wypłacona banknotami 100 zł, to kwota wypłacona banknotami 20 zł (ilość banknotów x wartość banknotu = kwota), kwota z warunków zadania.

II etap - zapisujemy równanie:

50x + 100 · 2x + 20(x + 2x - 4) = 850

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Mnożymy sumę przez 20. Redukujemy wyrazy podobne po lewej stronie. Przenosimy (-80) na prawą stronę - zmieniamy znak.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Ilość banknotów 50 zł, ilość banknotów 100 zł, ilość banknotów 20 zł, kwota wypłacona tymi banknotami. Kwota wypłacona z warunków zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Banknotów o wartości 20 zł było 5, o wartości 100 zł było 6, natomiast 3 banknoty miały wartość 50 zł.

Zadanie 10

4 cegły i 6 kg pierza ważą tyle samo co 6 cegieł i 2 kg żelaza. Ile waży 1 cegła?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Waga 1 cegły, waga 4 cegieł, waga 6 cegieł.

II etap - zapisujemy równanie:

Rozwiązywanie zadań tekstowych. Wyobraź sobie wagę z szalami - po 1 stronie 4 cegły i worek 6 kg, a po drugiej 6 cegieł i w kg żelaza.

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Przenosimy 6x na lewą stronę, 6 na prawą stronę - pamiętaj o zmianie znaków. Gdy dzielę 2 liczby ujemne, otrzymuję liczbę dodatnią.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. 1 cegła waży, 4 cegły ważą, 4 cegły + 6 kg pierza waży, 6 cegieł waży, 6 cegieł + 2 kg żelaza waży, czyli ważą tyle samo.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Jedna cegła waży 2 kg.

Zadanie 11

Ojciec ma 34 lata, a syn 2 lata. Za ile lat ojciec będzie 3 razy starszy od syna?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Poszukiwana liczba lat, tyle lat ojciec będzie miał za x lat, tyle lat będzie miał syn za x lat.

II etap - zapisujemy równanie:

Rozwiązywanie zadań tekstowych. Lewa strona jest trzy razy większa od prawej. Aby postawić znak =, trzeba prawą stronę pomnożyć przez 3.

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Po prawej stronie - sumę mnożymy przez 3 - każdy składnik. Przenosimy 3x na lewą stronę, 34 na prawą - ze zmienionymi znakami. Redukujemy wyrazy podobne, dzielimy obie strony przez (-2).

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Za 14 lat ojciec będzie miał - 34 + 14 = 48 lat

Za 14 lat syn będzie miał - 2 + 14 = 16 lat

Ojciec będzie trzy razy starszy, bo 3 · 16 = 48

V etap - zapisujemy odpowiedź:

Odpowiedź:

Za 14 lat ojciec będzie trzy razy starszy od syna.

Zadanie 12

W dwóch koszach są jabłka. W pierwszym jest dwa razy więcej niż w drugim. Gdyby z pierwszego przełożyć do drugiego 7 jabłek, to w obu byłoby tyle samo. Ile jest jabłek w każdym koszyku?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Ilość jabłek w II koszyku, ilość jabek w I koszyku (bo 2 razy więcej). 7 jabłek odbieramy, aby przełożyć do II koszyka, dokładamy 7 jabłek do II koszyka.

II etap - zapisujemy równanie:

w I koszyku jest 2x - 7

w II koszyku jest x + 7

w obu jest równa ilość jabłek, więc

2x - 7 = x + 7

III etap - rozwiązujemy równanie:

Przenosimy x z prawej na lewą stronę, (-7) na prawą, zmieniając znak. Redukujemy wyrazy podobne.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

W II koszyku jest 14 jabłek

W I koszyku jest 2 · 14 = 28 jabłek

Jeśli z I koszyka wyjmiemy 7 jabłek, to będzie 28 - 7 = 21

Jeśli do II koszyka dołożymy 7 jabłek, to będzie 14 + 7 = 21

Czyli w obu będzie tyle samo.

V etap - zapisujemy odpowiedź:

Odpowiedź:

W pierwszym koszyku jest 28 jabłek, a w drugim jest 14 jabłek.

Zadanie 13

W prostokącie o obwodzie 16 cm, jeden z boków jest o 4 cm krótszy od drugiego. Oblicz długości boków tego prostokąta.

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Długość jednego boku, drugi bok jest o 4 cm krótszy, to obwód prostokąta z warunków zadania.

II etap - zapisujemy równanie:

Rozwiązywanie zadań tekstowych. Obwód to suma wszystkich boków.

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Redukujemy wyrazy podobne po lewej stronie. Przenosimy (-8) na prawą stronę - zmieniamy znak. Dzielimy przez liczbę stojącą przy x.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Długość jednego boku prostokąta - 6 cm

Długość drugiego boku prostokąta - 6 - 4 = 2 cm

Obwód prostokąta - 2 · 6 + 2 · 2 = 12 + 4 = 16

Obwód z treści zadania - 16 cm

V etap - zapisujemy odpowiedź:

Odpowiedź:

Boki prostokąta mają 6 cm i 2 cm.

Zadanie 14

W trójkącie równoramiennym o obwodzie 15 cm, ramię jest 7 razy dłuższe od podstawy. Ile centymetrów ma podstawa, a ile ramię?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Ramię 7 razy większe - mnożymy przez 7. Obwód z warunków zadania.

II etap - zapisujemy równanie:

7x + 7x + x = 15

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Redukujemy wyrazy podobne po lewej stronie równania.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Podstawa, ramię, obwód z treści zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Podstawa ma 1 cm, a ramię 7 cm.

Zadanie 15

Oblicz długość wysokości trapezu, mając dane długości podstaw 5 cm, 7 cm, oraz pole równe 48 cm².

I etap - ustalamy niewiadomą:

Pole - 48 cm²

II etap - zapisujemy równanie:

Rozwiązywanie zadań tekstowych. Pole trapezu obliczamy.

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Dodaliśmy liczby w liczniku. Dzielimy przez liczbę stojącą przy niewiadomej.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Z warunków zadania.

etap V - zapisujemy odpowiedź:

Odpowiedź:

Wysokość trapezu wynosi 8 cm.

Zadanie 16

W trójkącie o polu 45 cm² wysokość ma długość 5 cm i dzieli podstawę trójkąta na dwa odcinki, z których jeden jest dwa razy dłuższy od drugiego. Jaką długość ma podstawa?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Pole trójkąta.

II etap - zapisujemy równanie:

Rozwiązywanie zadań tekstowych. Pole trójkąta obliczamy: 1/2 x podstawa x wysokość prostopadła do podstawy.

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Redukujemy wyrazy podobne w nawiasie. Wymnażamy lewą stronę. Dzielimy obie strony przez liczbę stojącą przy x. Znak : zastępujemy mnożeniem przez odwrotność drugiej liczby.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Długość podstawy, długość wysokości, pole.

Pole z warunków zadania - 45 cm²

V etap - zapisujemy odpowiedź:

Odpowiedź:

Podstawa trójkąta ma 18 cm.

Zadanie 17

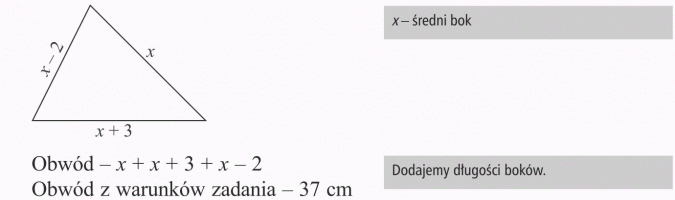
Obwód trójkąta wynosi 37 cm. Wiedząc, że jeden z boków jest o 3 cm dłuższy, a drugi o 2 cm krótszy od boku średniego, oblicz długości boków tego trójkąta.

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Obwód z warunków zadania, średni bok. Dodajemy długości boków.

II etap - zapisujemy równanie:

x + x + 3 + x - 2 = 37

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Redukujemy wyrazy podobne po lewej stronie. 1 przenosimy na prawą stronę ze zmienionym znakiem. Dzielimy obie strony przez 3.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Obwód z treści zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Boki tego trójkąta mają 12 cm, 10 cm, 15 cm.

Zadanie 18

Oblicz x, korzystając z rysunku:

Rozwiązywanie zadań tekstowych. Obliczamy trzeci kąt trójkąta. Trójkąt ma wszystkie kąty równe, po 60 st. każdy, jest to trójkąt równoboczny. Ma wszystkie boki równe.

II etap - zapisujemy równanie:

(2x - 1) = 3x - 2

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Przenosimy 3x na lewą stronę, (-1) na prawą - zmieniamy znaki. Dzielimy obie strony przez (-1).

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Bok AB ma długość 3 · 1 - 2 = 1 cm

Bok AC ma długość 2 · 1 - 1 = 1 cm

Boki są równe, bo trójkąt jest równoboczny.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Każdy bok ma 1 cm.

Zadanie 19

Suma trzech kolejnych liczb naturalnych wynosi 54. Znajdź te liczby.

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Pierwsza liczba, druga liczba, trzecia liczba. Każda następna liczba jest o 1 większa od poprzedniej.

II etap - zapisujemy równanie:

Rozwiązywanie zadań tekstowych. Bo suma tych liczb wynosi 54.

III etap - rozwiązanie równania

Rozwiązywanie zadań tekstowych. Redukcja wyrazów podobnych z lewej strony równania. Przenosimy 3 z lewej na prawą stronę - zmieniamy znak. Dzielimy obie strony przez liczbę stojącą przy niewiadomej.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. I liczba, II liczba, III liczba. Są to kolejne liczby. Suma tych liczb z treści zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Te liczby to: 17, 18, 19.

Zadanie 20

Różnica dwóch liczb wynosi 51,2. Jakie to liczby, jeżeli mniejsza stanowi 20% większej?

I etap - ustalamy niewiadomą:

Rozwiązywanie zadań tekstowych. Większa liczba, mniejsza liczba, różnica tych liczb, różnica tych liczb z warunków zadania.

II etap - zapisujemy równanie:

x - 20% x = 51,2

III etap - rozwiązujemy równanie:

Rozwiązywanie zadań tekstowych. Zamieniamy 4/5 na ułamek dziesiętny 0,8. Przesuwamy przecinek w obu liczbach o jedno miejsce w prawo.

IV etap - sprawdzamy, czy otrzymane rozwiązanie jest zgodne z treścią zadania:

Rozwiązywanie zadań tekstowych. Liczba. 20% liczby. Różnica liczb z warunków zadania.

V etap - zapisujemy odpowiedź:

Odpowiedź:

Szukane liczby to 64 i 12,8.

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Rozwiązywanie zadań tekstowych