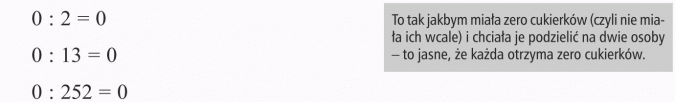Połączenie głosowe
Upewnij się, że masz włączone głośniki i mikrofon
zaprasza Cię do wspólnej nauki fiszek
Aby dzielenie było możliwe do wykonania, dzielnik nie może być równy zero!
Jeśli chcesz, by wynik był liczbą naturalną, dzielnik musi być mniejszy lub równy dzielnej i dzielić ją bez reszty.
W obliczeniach korzystasz z faktu, że dzielenie i mnożenie to działania odwrotne (wykorzystujesz tabliczkę mnożenia) oraz z prawa rozdzielności dzielenia względem dodawania.
Przykład
A teraz wytłumaczę Ci przykłady stosowania prawa rozdzielności dzielenia względem dodawania, które mówi, że dzieląc sumę przez daną liczbę możesz podzielić każdy składnik sumy przez tę liczbę, a otrzymane wyniki dodać.
Przykład
Ostatni przykład zawierał ciekawy przypadek: jeśli dzielnik jest równy dzielnej, to wynik z dzielenia wynosi jeden.
Przykład
Liczba zero może być dzielną i wtedy wynik dzielenia zawsze wynosi zero.
Przykład
DZIELENIE Z RESZTĄ
Osobna sprawa to sytuacja, kiedy w wyniku dzielenia otrzymujemy resztę niepodzielną przez dzielnik. Reszta jest zawsze mniejsza od dzielnika.
Przykład
Oblicz iloczyn liczb 15 i 8.
Rozwiązanie
Obliczyć iloczyn oznacza wykonać mnożenie.
Odp.:
Iloczyn liczb 15 i 8 wynosi 120.
Oblicz iloraz liczb 85 i 5.
Rozwiązanie
Obliczyć iloraz oznacza wykonać dzielenie, w którym liczba 85 jest dzielną a liczba 5 dzielnikiem.
Odp.:
Iloraz liczb 85 i 5 wynosi 17.
Rozwiąż równanie 3 · x = 27
Rozwiąż równania:
a) x : 7 = 6
b) 45 : y = 9
Rozwiązanie
W każdym przedziale wagonu 2 klasy jest 8 miejsc siedzących. Ile jest miejsc w 13 przedziałach?
Rozwiązanie
Odp.:
W 13 przedziałach są 104 miejsca siedzące.
Zosia ma 75 widokówek, a Ewa tylko 25. Ile razy więcej widokówek ma Zosia?
Odp.:
Zosia ma 3 razy więcej widokówek.
Na ławeczce może usiąść czworo dzieci. Czy wystarczy 7 ławeczek dla 30 dzieci?
Odp.:
7 ławeczek nie wystarczy dla 30 dzieci.
Teksty dostarczyło Wydawnictwo GREG. © Copyright by Wydawnictwo GREG
Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka
Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.
Ciekawostki (0)
Zabłyśnij i pokaż wszystkim, że znasz interesujący szczegół, ciekawy fakt dotyczący tego tematu.