Działania na liczbach naturalnych (na poziomie ucznia klasy 5)

Na początku przypomnę Ci, jak nazywają się liczby związane z działaniami:

Działania na liczbach naturalnych. Dodawanie, odejmowanie, mnożenie, dzielenie. Suma, różnica, iloczyn, iloraz. Składnik, odjemna, odjemnik, czynnik, dzielna, dzielnik.

W dodawaniu i mnożeniu mogą występować więcej niż dwa składniki lub odpowiednio czynniki. Oba te działania są przemienne i łączne, co wykorzystuję, ułatwiając sobie obliczenia.

Przykłady

Działania na liczbach naturalnych. Zmieniam kolejność składników, aby jedności dopełniały się do całych dziesiątek; dodaję otrzymane wyniki. Zmieniam kolejność czynników. Wykonuję mnożenie: 4 x 5 = 20.

Wynikiem dodawania lub mnożenia liczb naturalnych jest zawsze liczba naturalna.

Zwróć uwagę, że jeśli jeden ze składników jest równy zero - suma nie ulegnie zmianie.

Przykłady

138 + 0 = 138

0 + 28 = 28

3749 + 0 = 3749

Natomiast jeżeli choć jeden z czynników jest zerem, iloczyn wynosi zero!

Przykłady

0 · 15 = 0

1250 · 138 · 0 = 0

267 · 0 · 375 = 0

0 · 142 · 0 = 0

Pomnożenie liczby przez jeden daje zawsze w wyniku tę samą liczbę.

Przykłady

1 · 28 = 28

418 · 1 = 418

1 · 7652 = 7652

Nie wolno zmieniać kolejności liczb w odejmowaniu i dzieleniu!

Wynikiem odejmowania liczb naturalnych nie zawsze jest liczba naturalna.

Przykłady

Działania na liczbach naturalnych. Czytam: 19 należy do zbioru liczb naturalnych. Czytam: (-15) nie należy do zbioru liczb naturalnych. O liczach (-15) i (-100) opowiem w innym rozdziale.

Podsumowując: W wyniku odejmowania liczb naturalnych otrzymasz liczbę naturalną tylko wtedy, gdy odjemnik jest równy odjemnej lub mniejszy od niej.

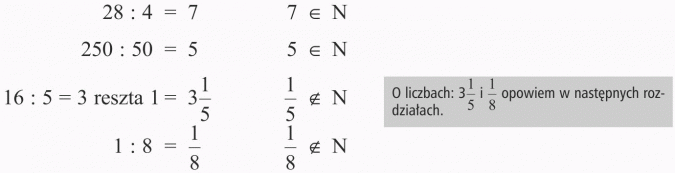
Dzielenie liczb naturalnych też nie zawsze daje w wyniku liczbę naturalną.

Przykłady

Działania na liczbach naturalnych. O liczbach 3 1/5 i 1/8 opowiem w następnych rozdziałach.

Podsumowując: Iloraz jest liczbą naturalną tylko wtedy, gdy dzielna jest wielokrotnością dzielnika (dzieli się bez reszty).

UWAGA!

Działania na liczbach naturalnych. 10 : 0. Dzielnikiem nie może być liczba zero! Takie dzielenie nie istnieje!

W klasie IV nauczyłeś się podnosić liczby naturalne do potęgi.

Potęgowanie to skrócony zapis mnożenia jednakowych czynników.

Działania na liczbach naturalnych. Czytam: trzy do potęgi drugiej lub trzy do kwadratu. Czytam: dwa do potęgi trzeciej lub dwa do sześcianu. Czytam: osiem do potęgi czwartej.

Zapis potęgi określa:

Działania na liczbach naturalnych. Ilość czynników, jaki jest czynnik.

Przykłady

7 · 7 · 7 = 7³

12 · 12 = 12²

15² = 15 · 15 = 225

8³ = 8 · 8 · 8 = 512

Wykonując działania na liczbach naturalnych, w zależności od potrzebi swoich możliwości, możesz posługiwać się obliczeniami pamięciowymi lub pisemnymi.

Przypomnę Ci najważniejsze zasady rachunku pisemnego. Pamiętaj, aby w dodawaniu i odejmowaniu liczby były odpowiednio podpisane, tzn. jedności pod jednościami, dziesiątki pod dziesiątkami itd.

Działania na liczbach naturalnych. Sumuję kolejne cyfry, rozpoczynając od jedności: 2 + 3 = 5, więc w rzędzie jedności wpisuję 5. Następnie dodaję cyfry dziesiątek: 5 + 7 = 12; wpisuję 2, a 1 (czyli 1 setkę) przenoszę do rzędu setek. Sumuję setki: 8 + 1 + 1 = 10, zapisuję 0, a 1 (czyli 1 tysiąc) przenoszę do rzędu tysięcy. Sumuję tysiące: 7 + 1 = 8, zapisuję w rzędzie tysięcy 8. Od 7 odejmuję 4, wynik wpisuję w rzędzie jedności. Od 0 nie mogę odjąć 8, więc pożyczam z rzędu setek 1 (czyli 10 dziesiątek), teraz odejmuję 10 - 8 = 2, wpisuję 2 w rzędzie dziesiątek. W rzędzie setek nie ma już 6 setek, tylko 5, więc odejmuję 5 - 2 = 3 i wpisuję wynik pod setkami.

Dodawanie i odejmowanie to działania odwrotne, dlatego odejmowanie zawsze możesz sprawdzić, dodając różnicę (323) do odjemnika (284). Jeżeli otrzymałeś odjemną (607), to działanie zostało wykonane poprawnie.

Przykład

Działania na liczbach naturalnych. Odjemna, odjemnik, różnica. spr. tak w skrócie zapisuje się: sprawdzenie. Odejmowanie wykonane poprawnie!

Mnożenie pisemne zapisujesz tak, aby obliczenia maksymalnie uprościć:

Działania na liczbach naturalnych. Najpierw mnożę 512 przez 8, czyli: 8 x 2 = 16, wpisuję 6 pod jednościami, a 1 (1 dziesiątkę) dodaję do wyniku z mnożenia dziesiątek, czyli 8 x 1 = 8; 8 + 1 = 9, więc wpisuję 9 pod dziesiątkami; 5 x 8 - 40, więc pod setkami wpisuję 0, a 4 w wyższym rzędzie (rzędzie tysięcy). Teraz mnożę 512 przez 1 (a właściwie przez 10). 1 x 2 = 2 - wpisuję pod dziesiątkami. 1 x 1 = 1 - wpisuję pod setkami. 1 x 5 = 5 - wpisuję pod tysiącami. Wyniki z obu mnożeń dodaję.

Wykonując mnożenie pisemne, możesz korzystać z wielu ułatwień, pozwalających na szybsze obliczenie wyniku.

Przykłady

Działania na liczbach naturalnych. Ponieważ mnożenie przez 0 daje w wyniku 0, przesuwam liczby i wykonuję mnożenie 418 x 37, a trzy zera dopisuję do wyniku po prawej stronie. Nie wykonuję mnożenia przez 0! Mnożę 315 przez 6 (jedności), a później przez 3 (setki) i odpowiednio podpisuję wyniki - zaczynam wpisywać cyfry pod setkami.

Dzielenie pisemne wykonuj w ten sposób:

Działania na liczbach naturalnych. Dzielenie rozpoczynam od lewej strony dzielnej. 1 nie mogę podzielić przez 8, więc biorę następną cyfrę i próbuję dzielić. W 13 liczba 8 mieści się 1 raz - jeden wpisuję nad trójką (nad kreską), wynik z mnożenia 1 x 8 = 8 odejmuję od 13 (reszta 5). Spisuję 8, dzielę 58 : 8 = 7 r 2, zapisuję 7 nad 8, odejmuję 58 - 56 = 2 (7 x 8 = 56). Spisuję 4, dzielę 24 : 8 = 3 - zapisuję 3 nad 4, 24 - 24 = 0 - zakończyłam dzielenie.

Mnożenie i dzielenie to działania odwrotne, dlatego wynik dzielenia zawsze możesz sprawdzić za pomocą mnożenia.

Działania na liczbach naturalnych. Mnożę iloraz (173) przez dzielnik (8) i powinnam otrzymać dzielną (1384). Poprzednie dzielenie wykonałam poprawnie!

W dzieleniu pisemnym również możesz korzystać z ułatwień.

Przykład

Działania na liczbach naturalnych. Ponieważ dzielna i dzielnik zakończone są zerami, skreślam w obu liczbach po dwa zera i wykonuję dzielenie 9180 : 54. UWAGA: Po odjęciu 378 - 378 = 0 zostało do spisania 0, ale 0 : 54 = 0, więc od razu nad kreską zapisuję 0. Pamiętam, że 170 to wynik dzielenia 918000 przez 5400, zatem sprawdzam, mnożąc iloraz (170) przez dzielnik (5400). Dzielenie zostało wykonane poprawnie!

Pamiętaj!

W dzielnej i dzielniku możesz skreślić jednakową liczbę zer.

Zadanie 1

Znajdź liczbę:

a) o 25 mniejszą od iloczynu liczb 56 i 48;

b) o 7 większą od ilorazu liczb 3600 i 150;

c) 2 razy większą od różnicy liczb 4008 i 289;

d) 3 razy mniejszą od sumy liczb 592 i 95.

Rozwiązanie:

Działania na liczbach naturalnych. Obliczam iloczyn 56 i 48. Obliczam liczbę o 25 mniejszą.

Odpowiedź:

Szukana liczba to 2663.

Działania na liczbach naturalnych. Obliczam iloraz liczb 3600 i 150. Obliczam liczbę o 7 większą.

Odpowiedź:

Szukana liczba to 31.

Działania na liczbach naturalnych. Obliczam różnicę liczb 4008 i 289. Sprawdzam poprawność odejmowania. Obliczam liczbę 2 razy większą.

Odpowiedź:

Szukana liczba to 7438.

Działania na liczbach naturalnych. Obliczam sumę liczb 592 i 95. Obliczam liczbę 3 razy mniejszą.

Odpowiedź:

Szukana liczba to 229.

Zadanie 2

Słoń waży 4 tony, a Ola tylko 20 kilogramów (kg). Ile razy słoń jest cięższy od Oli?

Rozwiązanie:

Działania na liczbach naturalnych. Tony zamieniam na kilogramy; 1 t = 1000 kg. Aby obliczyć ile razy słoń jest cięższy od Oli, dzielę masę słonia przez masę Oli. Sprawdzam: 200 x 20 = 4000 (mnożę 2 x 2 = 4 i dopisuję 3 zera).

Odpowiedź:

Słoń jest 200 razy cięższy od Oli.

Zadanie 3

Do dwóch szkół uczęszcza 1240 uczniów. W pierwszej szkole jest 705 uczniów. Oblicz, w której szkole jest więcej uczniów i o ile?

Rozwiązanie:

Działania na liczbach naturalnych. Aby dowiedzieć się ilu uczniów jest w drugiej szkole, od całkowitej liczby uczniów odejmuję liczbę uczniów z pierwszej szkoły. W drugiej szkole jest 535 uczniów. Liczby mają tyle samo cyfr, więc porównuję cyfry setek 7 > 5. Obliczam, o ile liczba uczniów w pierwszej szkole jest większa od liczby uczniów w drugiej szkole.

Odpowiedź:

W pierwszej szkole jest o 170 uczniów więcej niż w drugiej.

Autorzy opracowań: B. Wojnar, B. Włodarczyk, A Sabak, D. Stopka, A Szostak, D. Pietrzyk, A. Popławska, E. Seweryn, M. Zagnińska, J. Paciorek, E. Lis, M. D. Wyrwińska, A Jaszczuk, A Barszcz, A. Żmuda, K. Stypinska, A Radek, J. Fuerst, C. Hadam, I. Kubowia-Bień, M. Dubiel, J. Pabian, M. Lewcun, B. Matoga, A. Nawrot, S. Jaszczuk, A Krzyżek, J. Zastawny, K. Surówka, E. Nowak, P. Czerwiński, G. Matachowska, B. Więsek, Z. Daszczyńska, R. Całka

Zgodnie z regulaminem serwisu www.opracowania.pl, rozpowszechnianie niniejszego materiału w wersji oryginalnej albo w postaci opracowania, utrwalanie lub kopiowanie materiału w celu rozpowszechnienia w szczególności zamieszczanie na innym serwerze, przekazywanie drogą elektroniczną i wykorzystywanie materiału w inny sposób niż dla celów własnej edukacji bez zgody autora jest niedozwolone.

Wybierz treść

Wybierz szkołę

Wybierz przedmiot

Wybierz dział

Opracowania

Działania na liczbach naturalnych (na poziomie ucznia klasy 5)